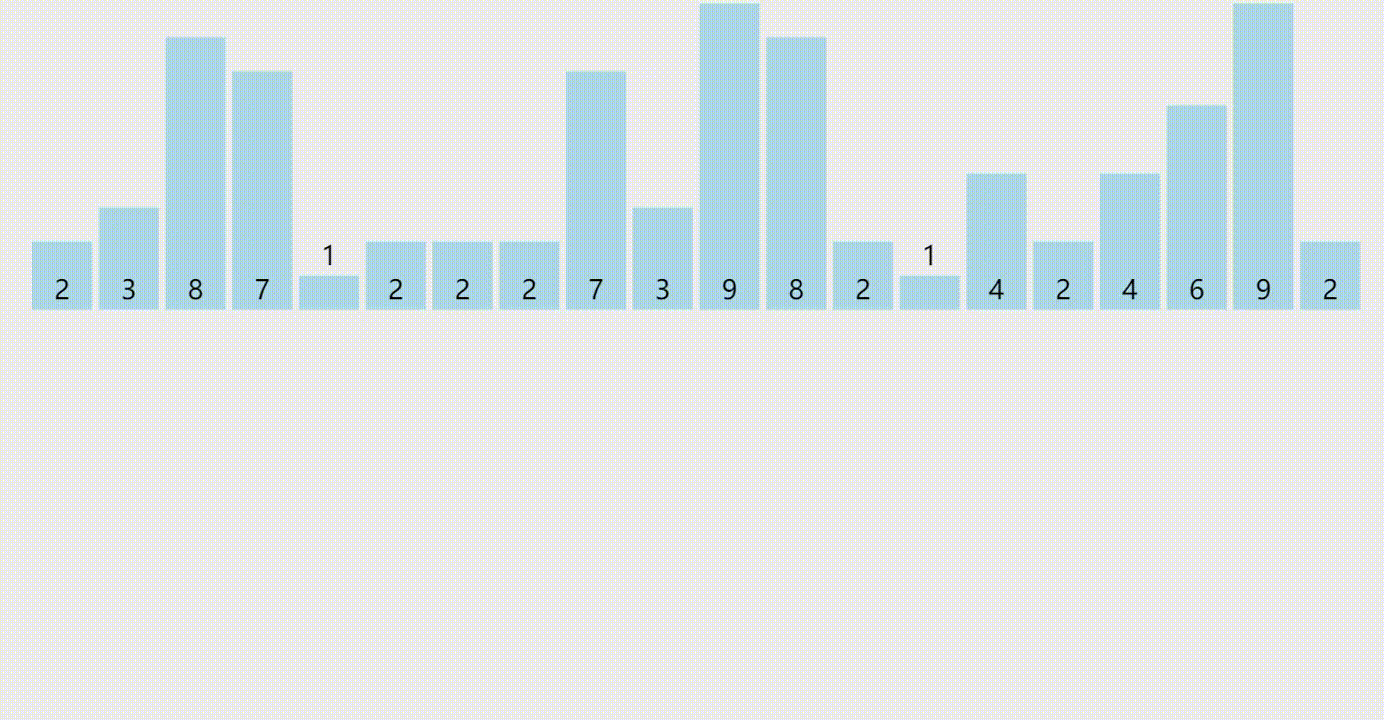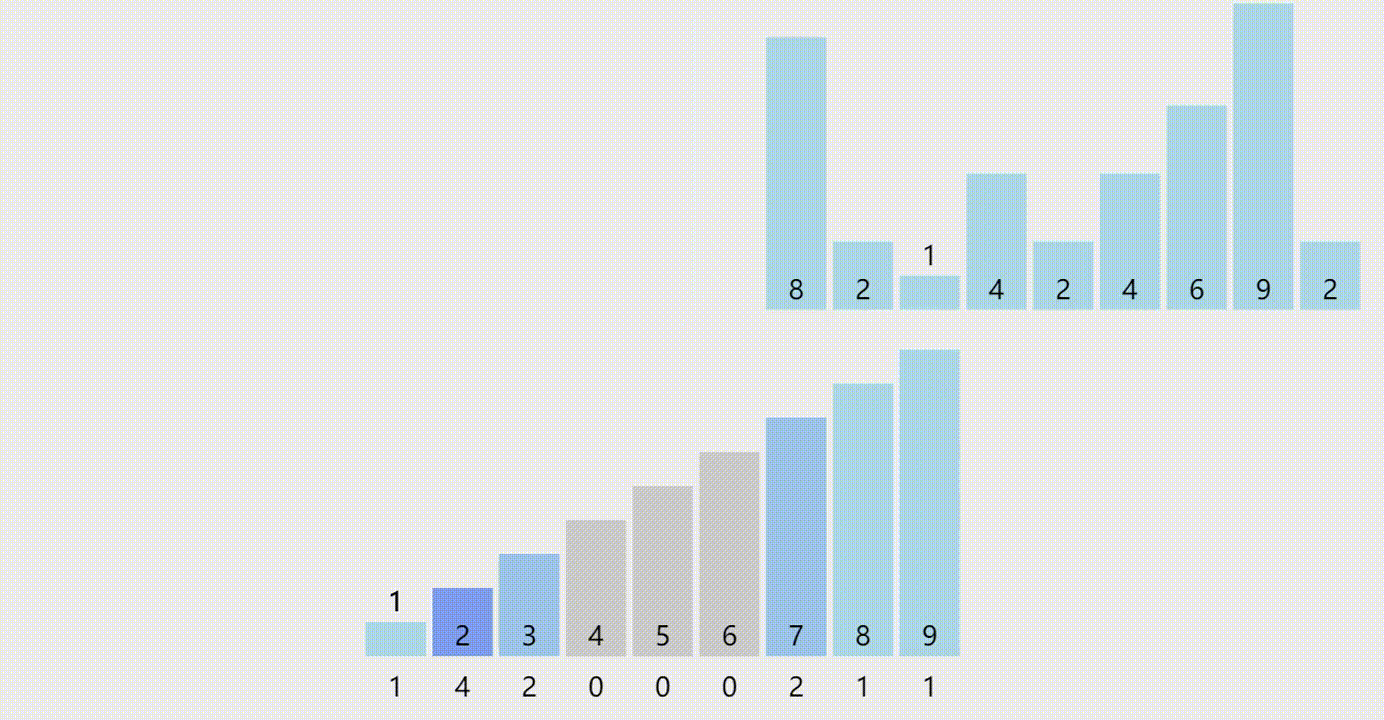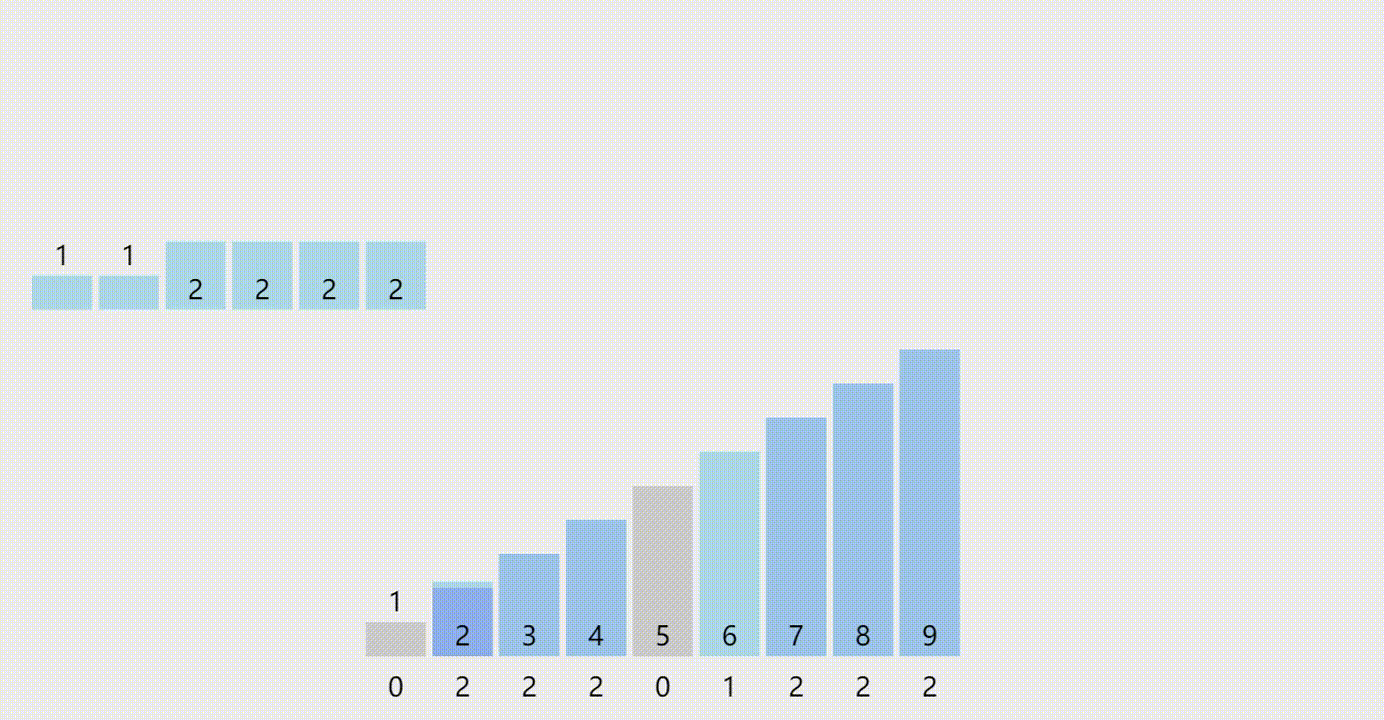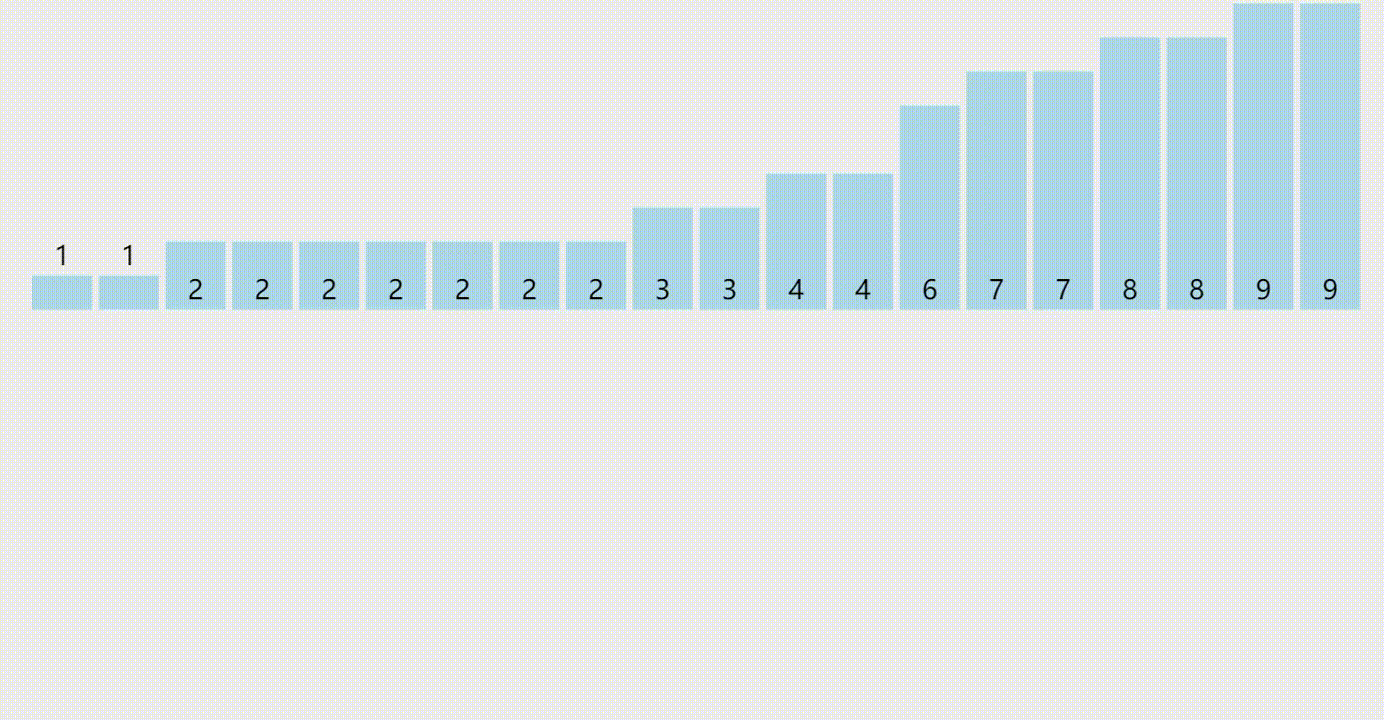4、常见排序算法
术语解释:
1、稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 仍然在 b 的前面,则为稳定排序。
2、非稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为非稳定排序。
3、原地排序:原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
4、非原地排序:需要利用额外的数组来辅助排序。
5、时间复杂度:一个算法执行所消耗的时间。
6、空间复杂度:运行完一个算法所需的内存大小。
常见的排序算法
常见的排序算法有:
- 冒泡排序:通过不断交换相邻的元素,使得较大的元素慢慢“浮”到数列的顶端。
- 选择排序:通过不断地选择剩余元素中的最小值,使得排序的效率更高。
- 插入排序:通过不断地将未排序的元素插入到已排序的序列中,使得整个序列有序。
- 快速排序:通过分治法,对数列进行快速排序。
- 归并排序:通过分治法,将数列不断分成两半,最终合并成一个有序的序列。
- 堆排序:通过利用堆的性质,对数列进行排序。
- 计数排序:通过统计每个数字在数列中出现的次数,实现排序的效果。
- 桶排序:通过建立一个桶,将数字分配到对应的桶中,最终得到排序结果。
这只是排序算法的一部分,排序算法的数量和种类仍在不断增加。根据不同的应用领域,也有不同的排序算法。
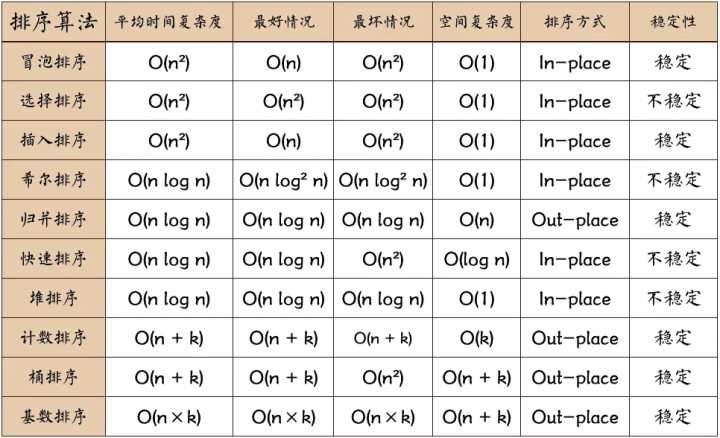
常见排序算法的时间复杂度
以下是各种常见排序算法的时间复杂度:
- 冒泡排序:平均情况O(n2),最坏情况O(n2),最好情况O(n),空间复杂度O(1)。
- 选择排序:平均情况O(n2),最坏情况O(n2),最好情况O(n2),空间复杂度O(1)。
- 插入排序:平均情况O(n2),最坏情况O(n2),最好情况O(n),空间复杂度O(1)。
- 快速排序:平均情况O(nlogn),最坏情况O(n2),最好情况O(nlogn),空间复杂度O(nlogn)~O(n)。
- 归并排序:平均情况O(nlogn),最坏情况O(nlogn),最好情况O(nlogn),空间复杂度O(n)。
- 堆排序:平均情况O(nlogn),最坏情况O(nlogn),最好情况O(nlogn),空间复杂度O(1)。
- 计数排序:平均情况O(n+k),最坏情况O(n+k),最好情况O(n+k),空间复杂度O(k)。
- 桶排序:平均情况O(n+k),最坏情况O(n2),最好情况O(n),空间复杂度O(n+k)。
- 希尔排序:平均情况O(n1.3-n2),最坏情况O(n2)
排序算法的稳定性说明
排序算法的稳定性指的是经过排序后,相同元素在序列中的相对顺序不变。
例如,如果有两个数5和3,经过排序后,两个数的相对顺序不变。
常见的稳定排序算法有:冒泡排序,插入排序,归并排序,基数排序。
不稳定的排序算法有:选择排序,快速排序,希尔排序,堆排序。
稳定性对于排序的实际应用很重要,因为它决定了相同元素在排序后的相对位置。有时候,稳定性可以有助于解决一些排序后元素相对位置的问题。
冒泡排序
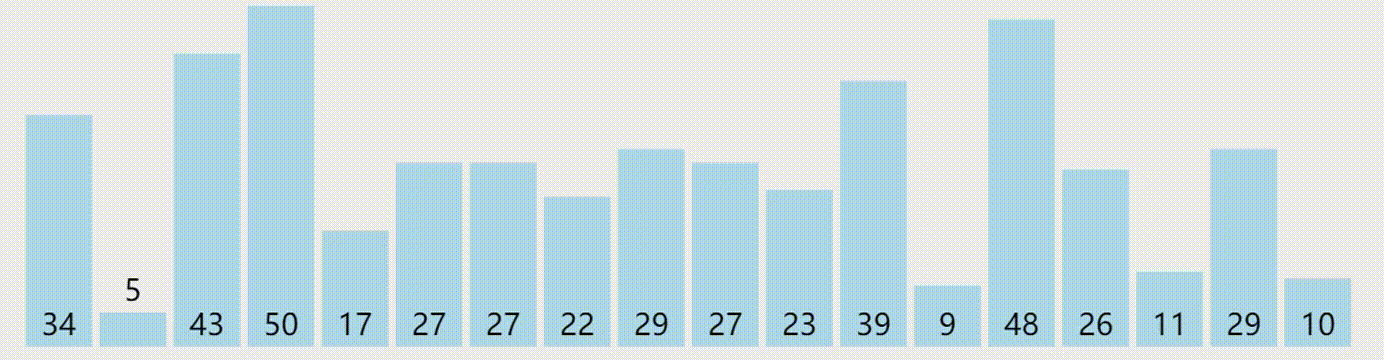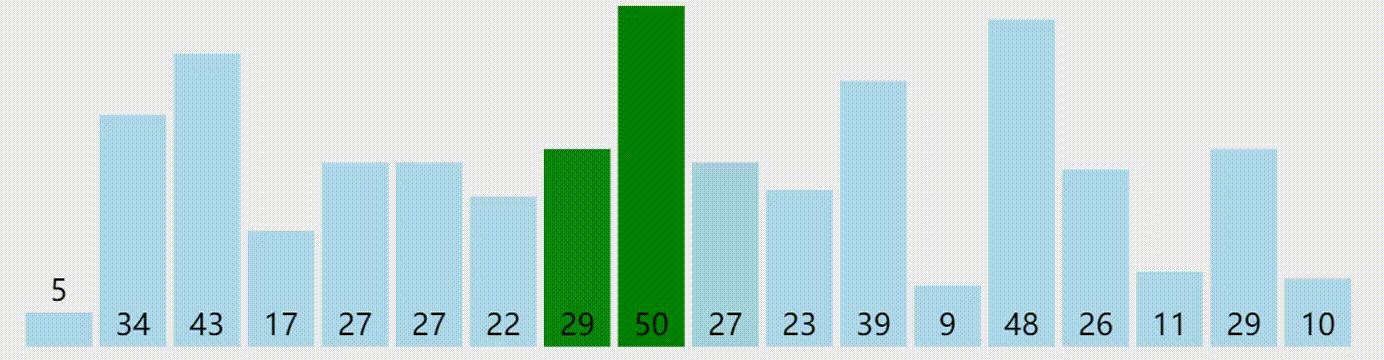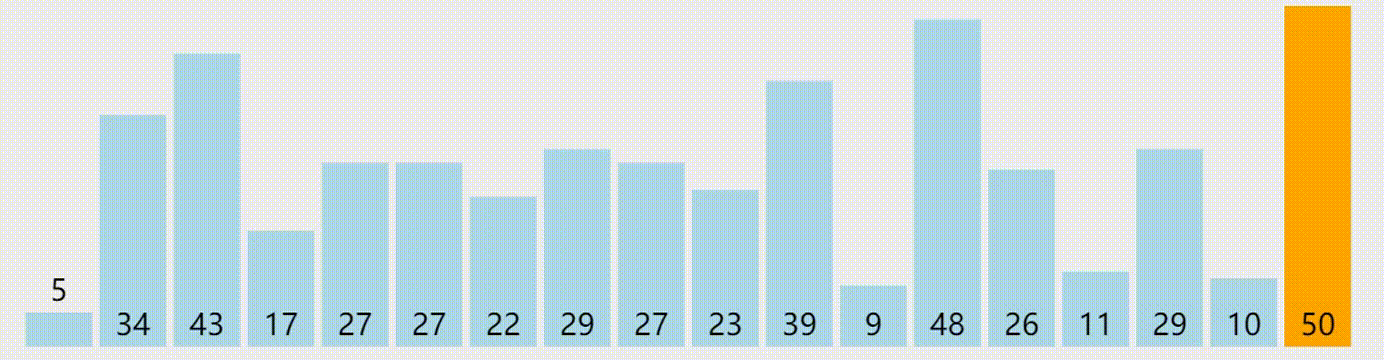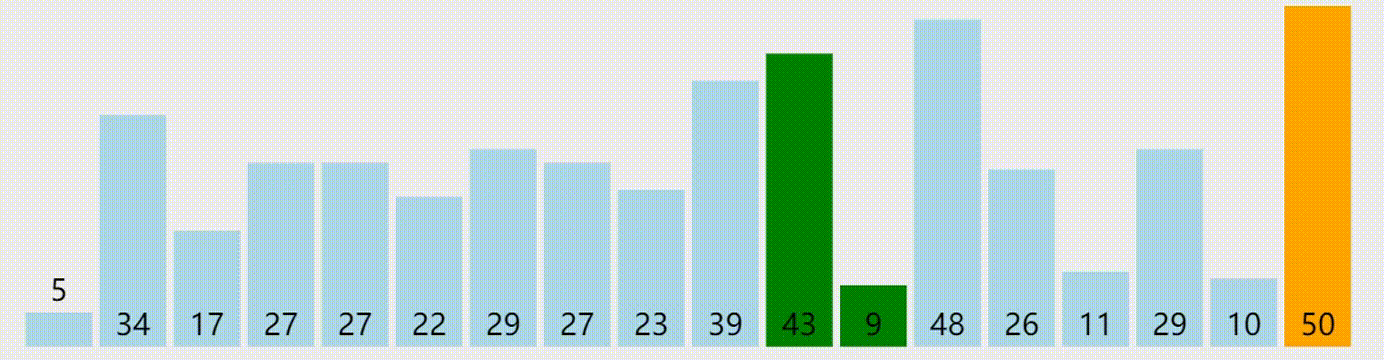
下面是一个冒泡排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | #include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
bubbleSort(arr, n);
cout << "\nSorted array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了冒泡排序的基本功能:在给定的数组上进行排序,最终得到一个从小到大的有序数组。
选择排序
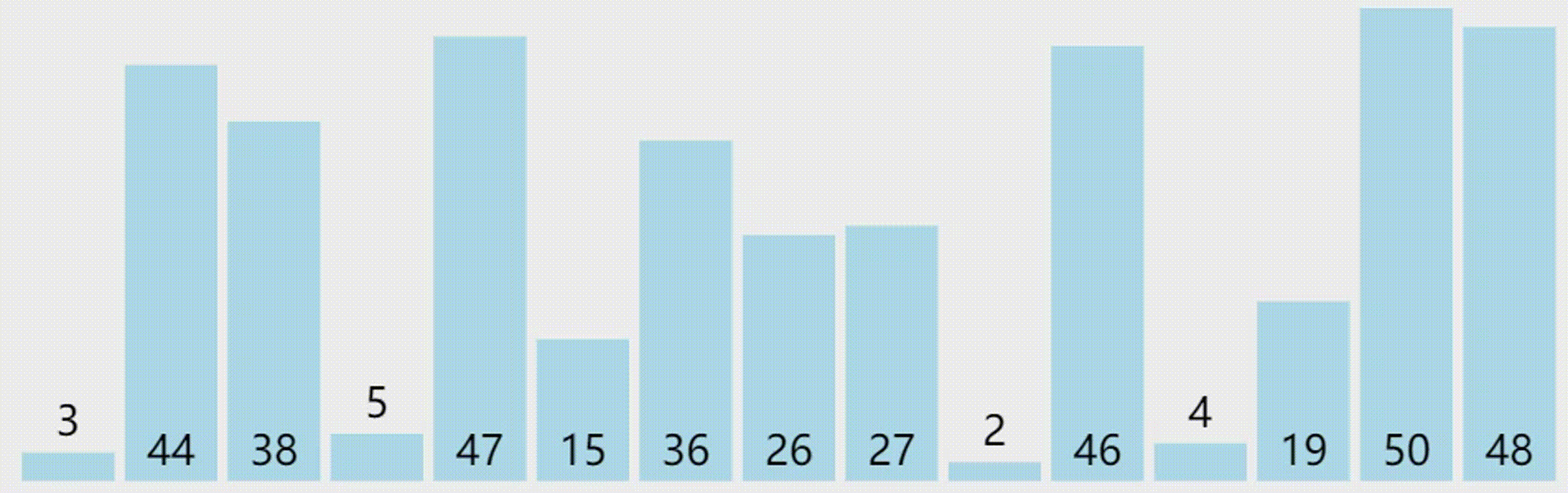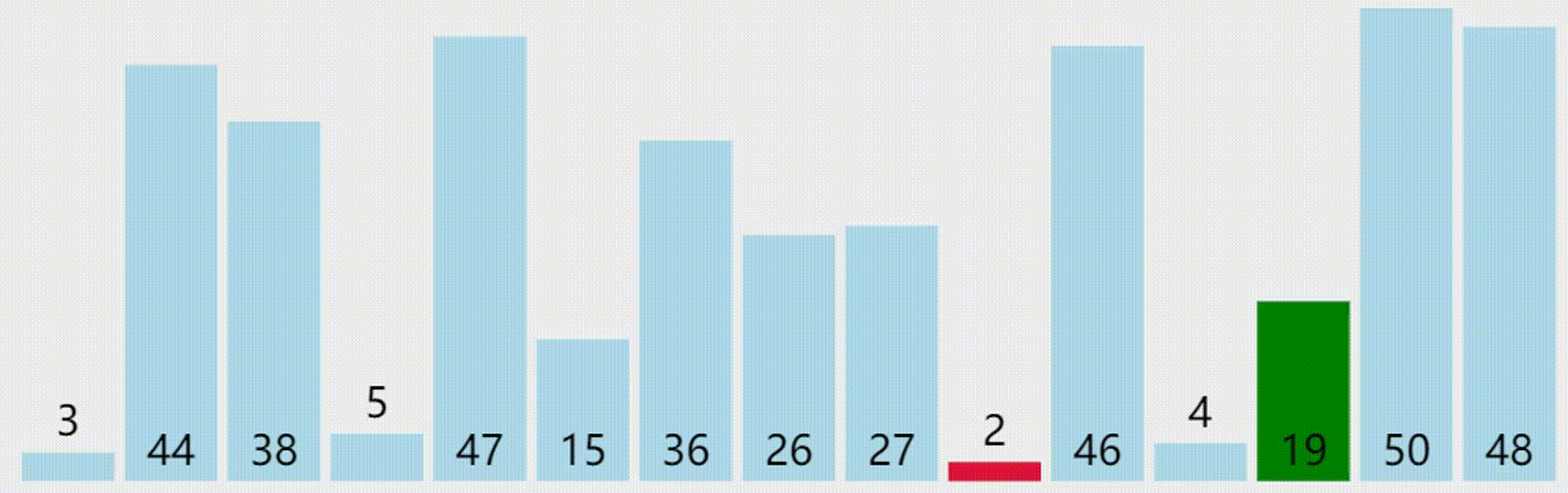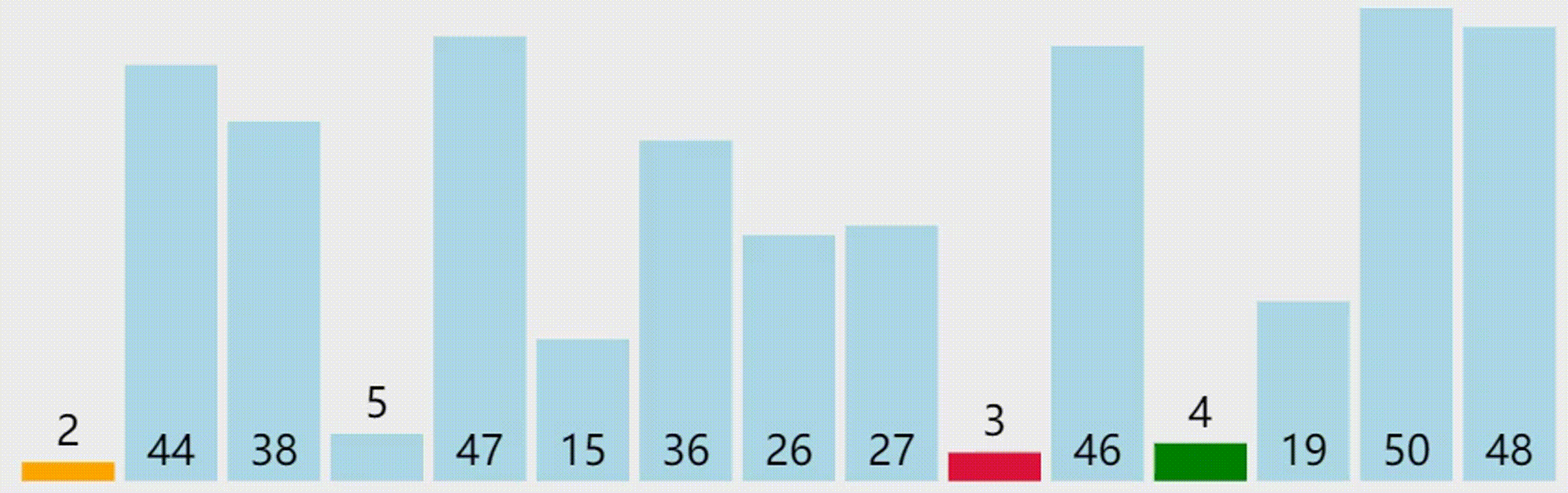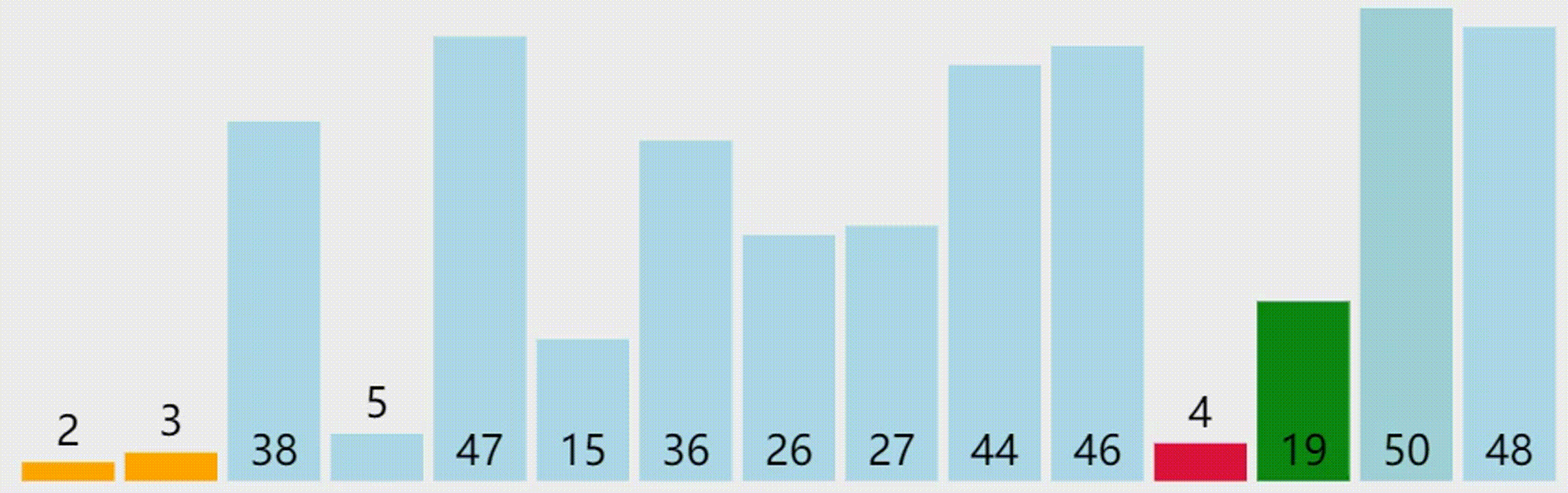
下面是一个选择排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | #include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
int i, j, minIndex, temp;
for (i = 0; i < n-1; i++) {
minIndex = i;
for (j = i+1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
int main() {
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
selectionSort(arr, n);
cout << "\nSorted array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了选择排序的基本功能:在给定的数组上进行排序,最终得到一个从小到大的有序数组。
插入排序
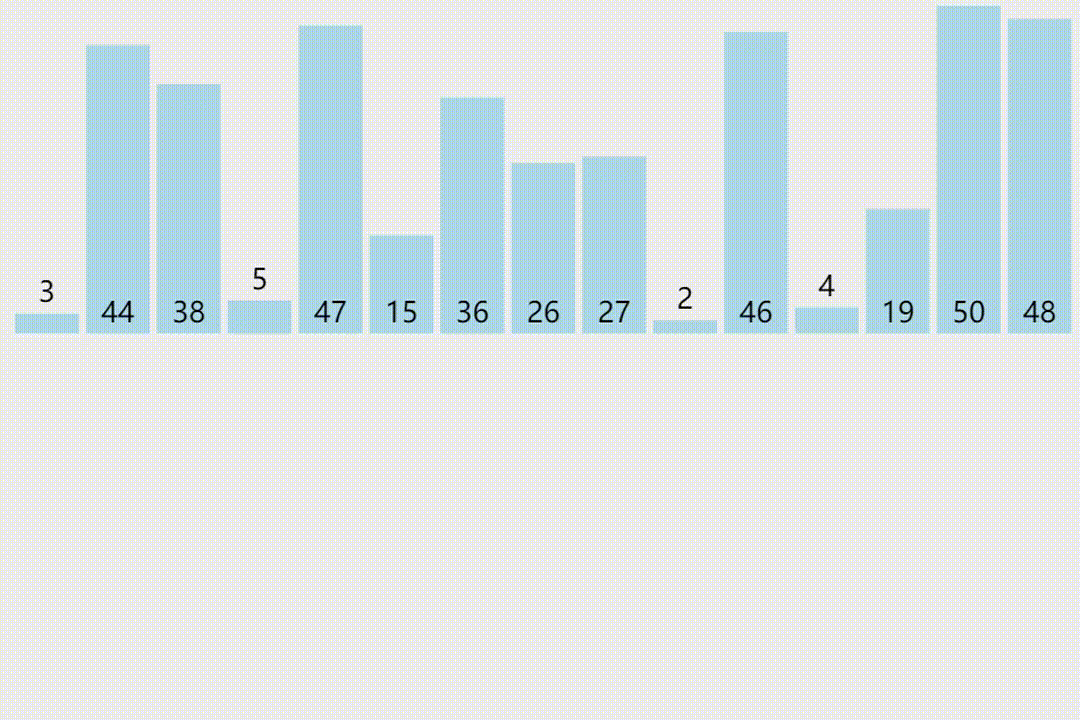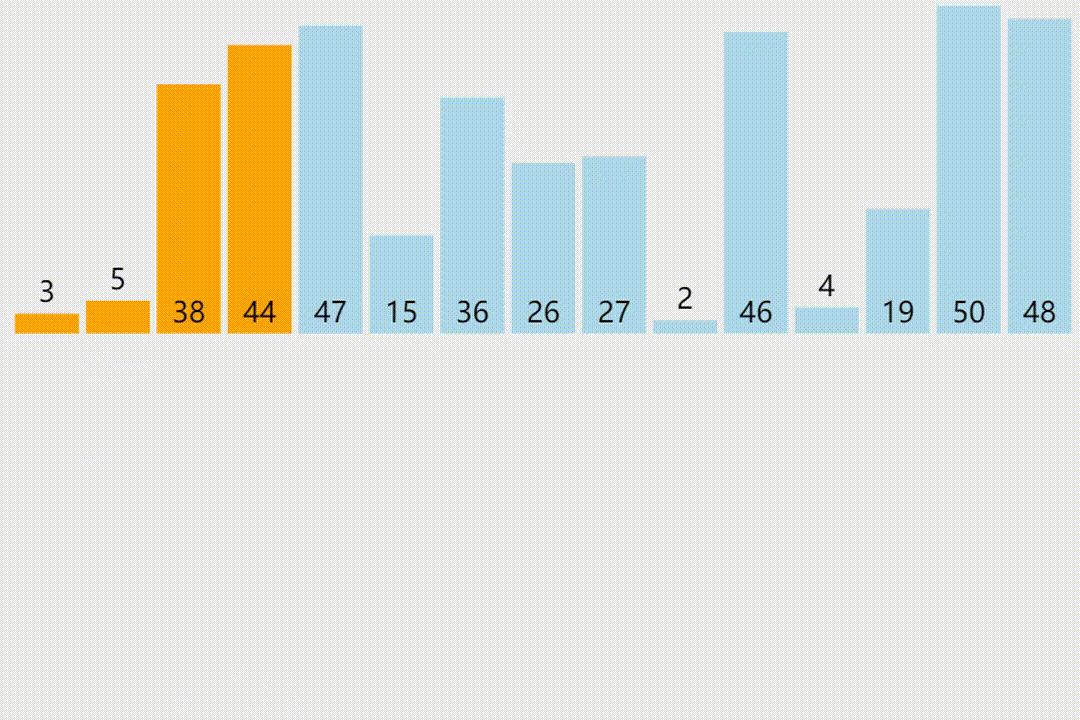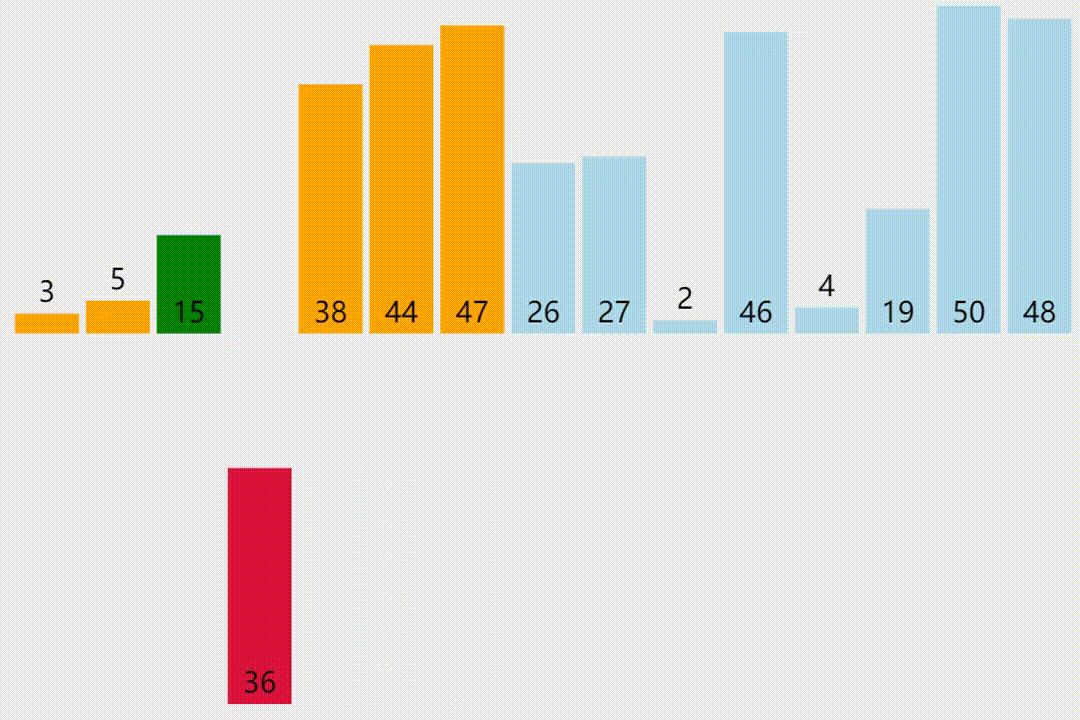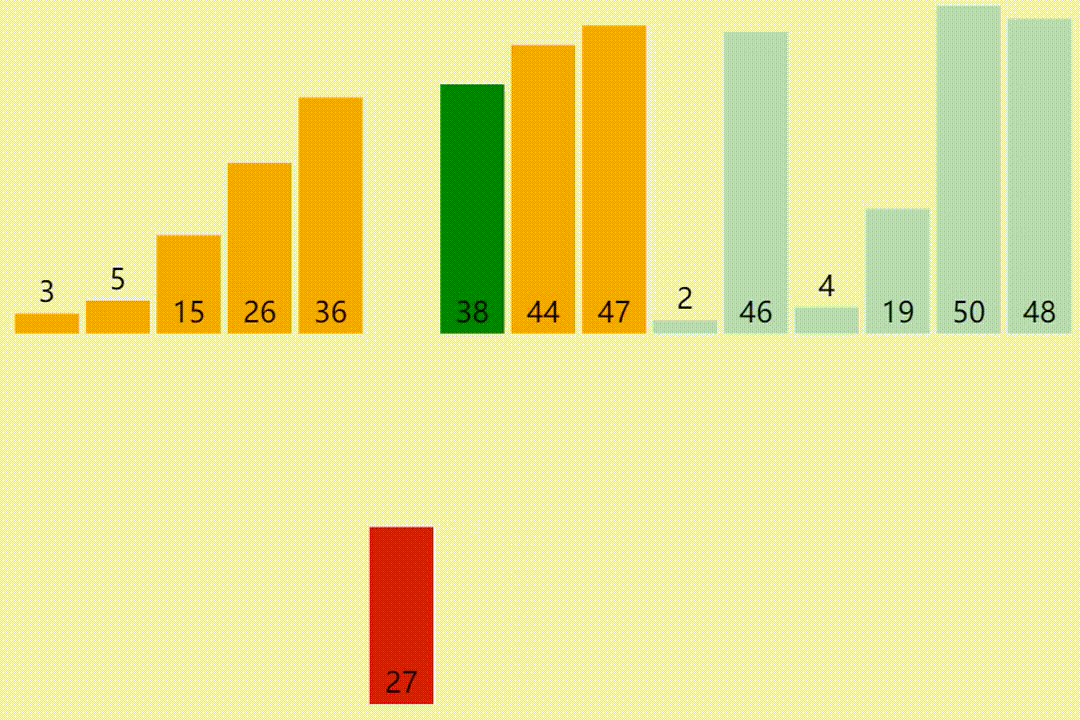
下面是一个插入排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | #include <iostream>
using namespace std;
void insertionSort(int arr[], int n) {
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
insertionSort(arr, n);
cout << "\nSorted array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了插入排序的基本功能:在给定的数组上进行排序,最终得到一个从小到大的有序数组。
快速排序

快速排序的原理
快速排序是一种分治的排序算法。它采用了一种分而治之的策略,将大问题分成小问题分别解决,递归地对整个序列进行排序。
快速排序的基本思想是:从数列中挑选一个元素(称为“基准元素”),将数列分成两部分,一部分比基准元素小,一部分比基准元素大;然后再按照这种方法对两个部分分别进行快速排序,整个数列就有序了。
快速排序的实现方法如下:首先,选择数列的第一个元素作为基准元素;然后从数列的两端向中间扫描,将小于基准元素的元素放到左端,大于基准元素的元素放到右端;对于基准元素左右两个子序列,不断地递归地进行快速排序,直到所有子序列都有序。
下面是一个快速排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 | #include <iostream>
using namespace std;
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
if (arr[j] <= pivot) {
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i + 1], arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
quickSort(arr, 0, n - 1);
cout << "\nSorted array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了快速排序的基本功能:在给定的数组上进行排序,最终得到一个从小到大的有序数组。
归并排序
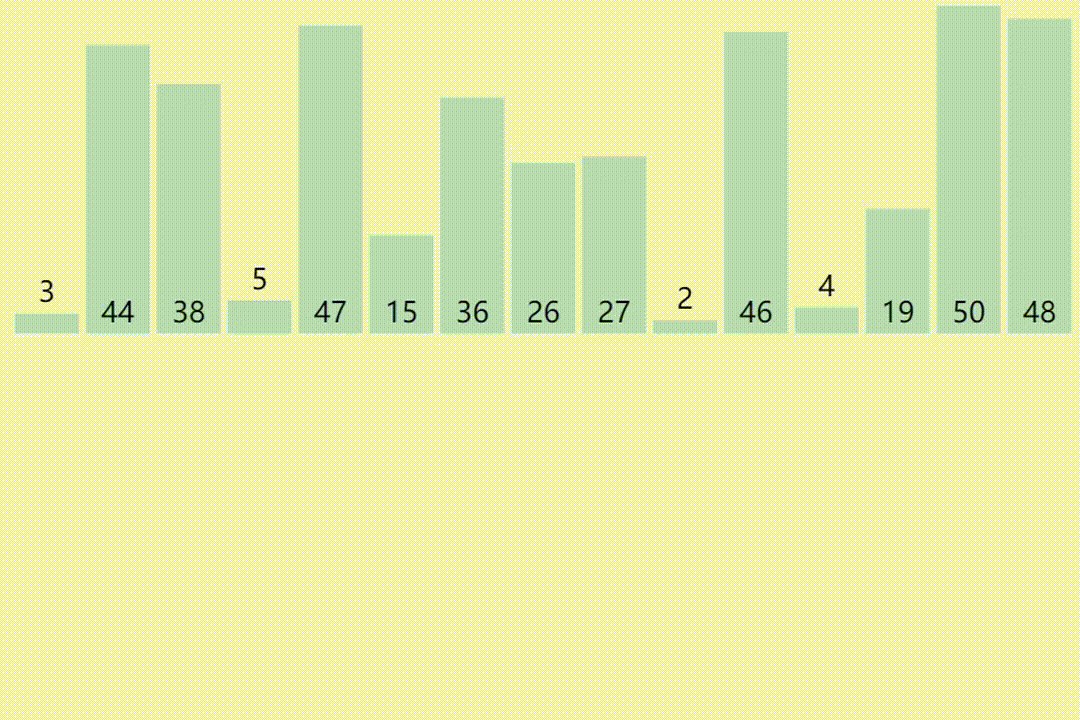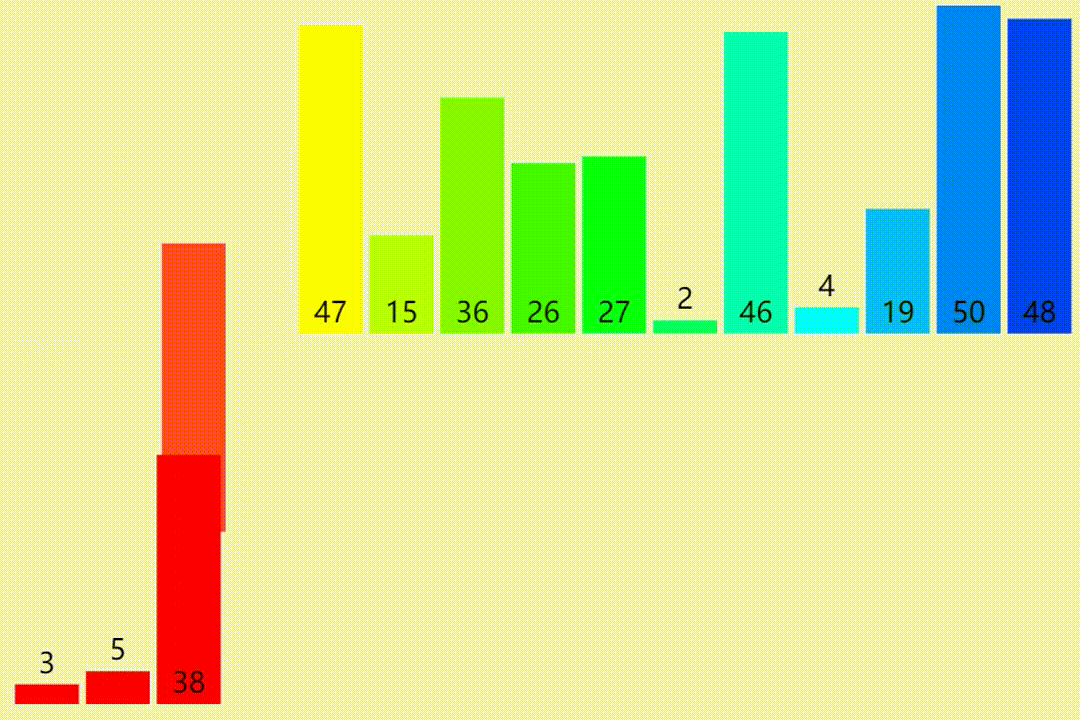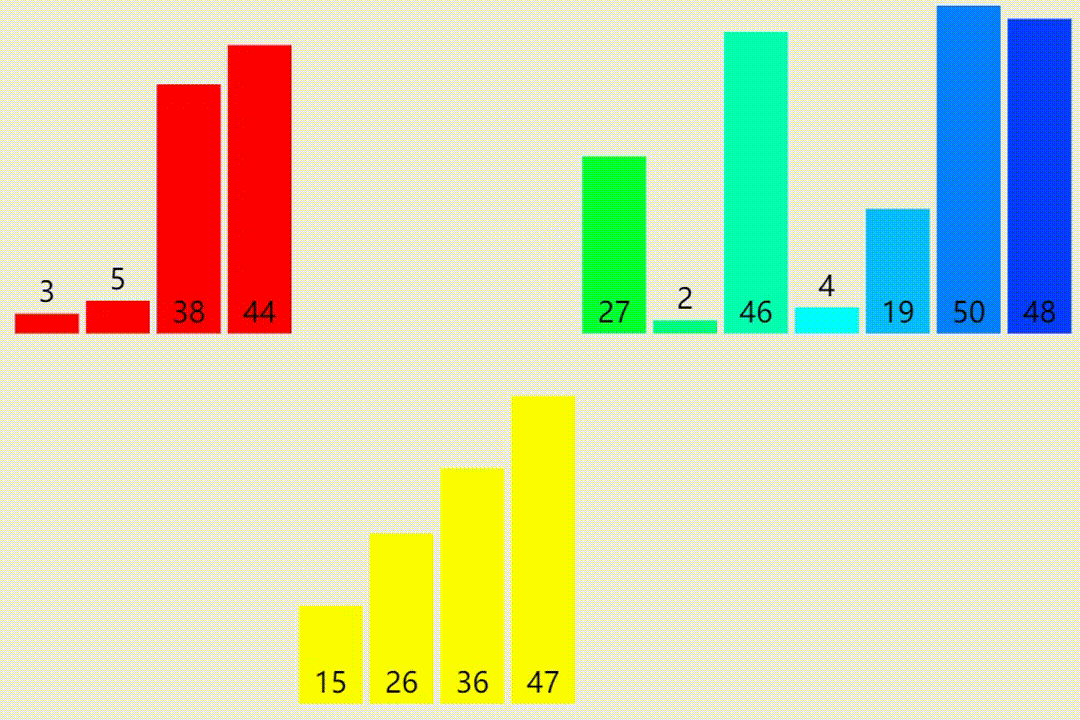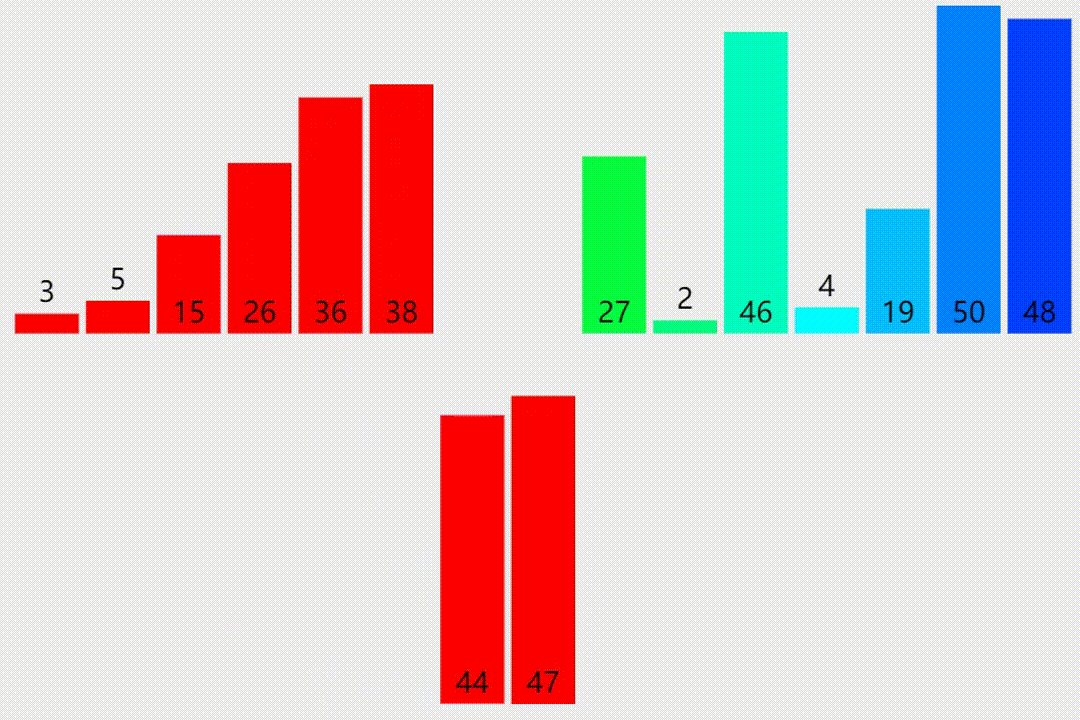
归并排序的原理
归并排序是一种分治的排序算法。它采用了一种分而治之的策略,将大问题分成小问题分别解决,递归地对整个序列进行排序。
归并排序的基本思想是:将数列分成两个子序列,分别对两个子序列进行排序,再将排好序的两个子序列合并成一个有序序列。
归并排序的实现方法如下:首先,将整个数列从中间分开,分别对左右两个子序列进行排序;然后将两个排好序的子序列合并成一个有序序列,这个过程可以用递归实现,也可以用迭代实现。归并排序的时间复杂度为O(nlogn),是一种高效的排序算法。
下面是一个归并排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 | #include <iostream>
using namespace std;
void merge(int arr[], int l, int m, int r) {
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (i = 0; i < n1; i++) {
L[i] = arr[l + i];
}
for (j = 0; j < n2; j++) {
R[j] = arr[m + 1 + j];
}
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
mergeSort(arr, 0, n - 1);
cout << "\nSorted array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了归并排序的基本功能:在给定的数组上进行排序,最终得到一个从小到大的有序数组。
堆排序

堆排序的原理
堆排序是一种选择排序算法,它的核心思想是:利用堆的性质(堆是一棵完全二叉树,每个结点都大于等于或小于等于它的子结点),在排序的过程中不断地取出堆顶元素,直到堆为空。
堆排序的基本步骤如下:
- 构造一个堆,通常是大根堆或小根堆。
- 将堆顶元素与堆底元素交换,并在堆中删除堆顶元素。
- 重新调整堆的结构,使其重新满足堆的性质。
- 重复2、3步,直到堆为空。
堆排序的时间复杂度为O(nlogn),因为每次交换堆顶元素和堆底元素都需要重新调整堆的结构,需要O(logn)的时间复杂度,故总的时间复杂度为O(nlogn)。
下面是一个堆排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | #include <iostream>
using namespace std;
void heapify(int arr[], int n, int i) {
int largest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
if (l < n && arr[l] > arr[largest]) {
largest = l;
}
if (r < n && arr[r] > arr[largest]) {
largest = r;
}
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
void heapSort(int arr[], int n) {
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
heapSort(arr, n);
cout << "\nSorted array: \n";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了堆排序的基本功能:在给定的数组上进行排序,最终得到一个从小到大的有序数组。
计数排序
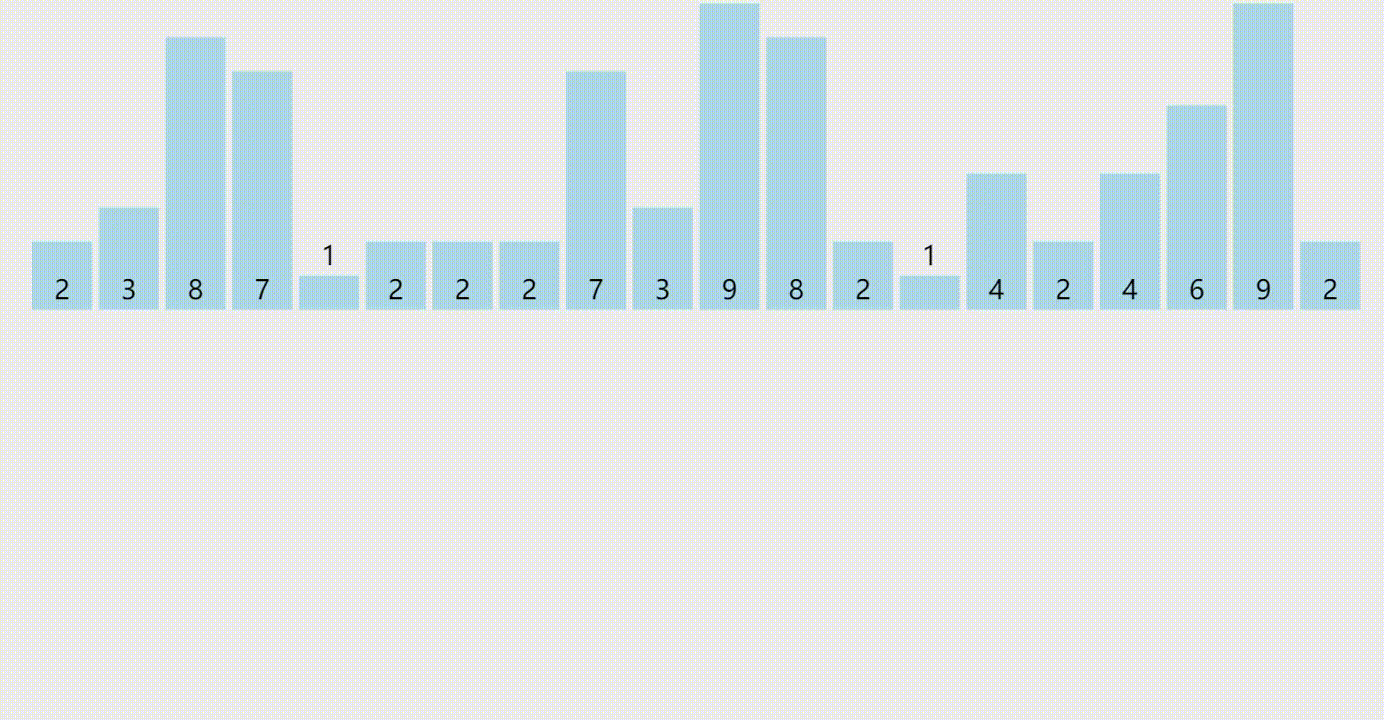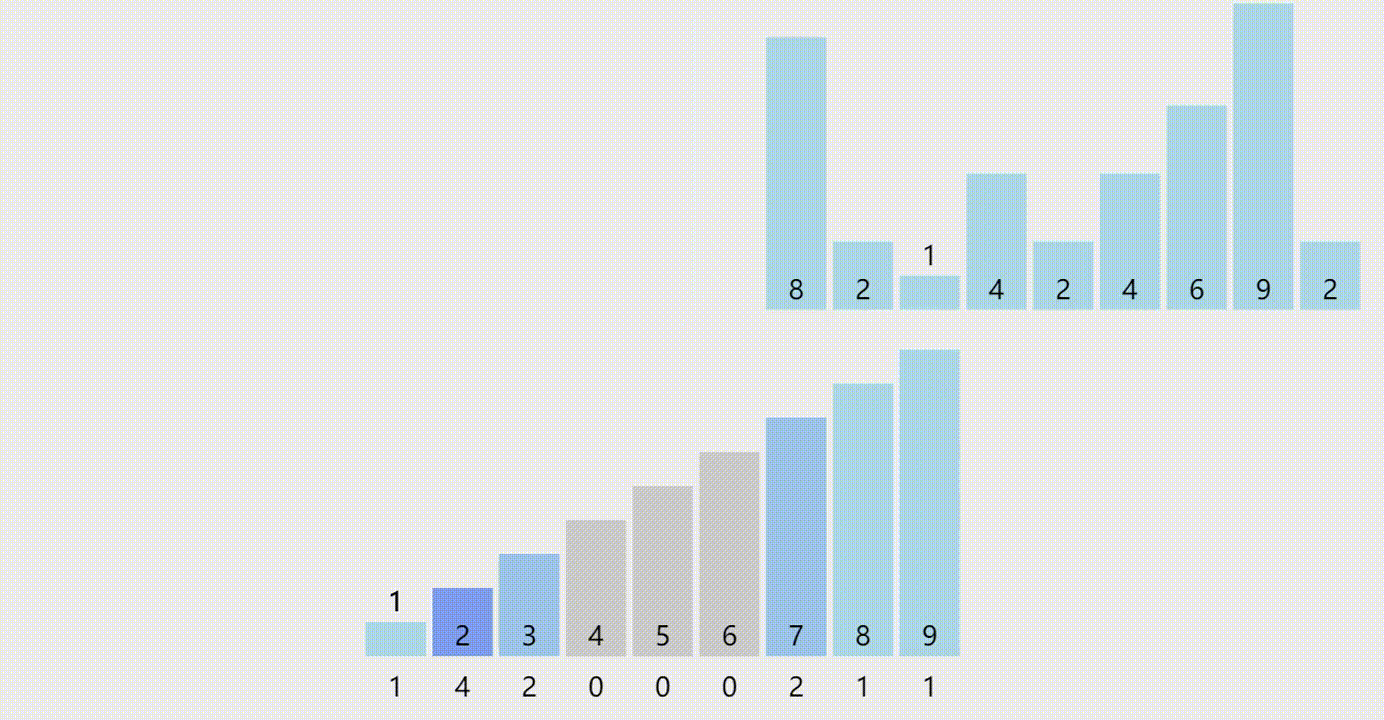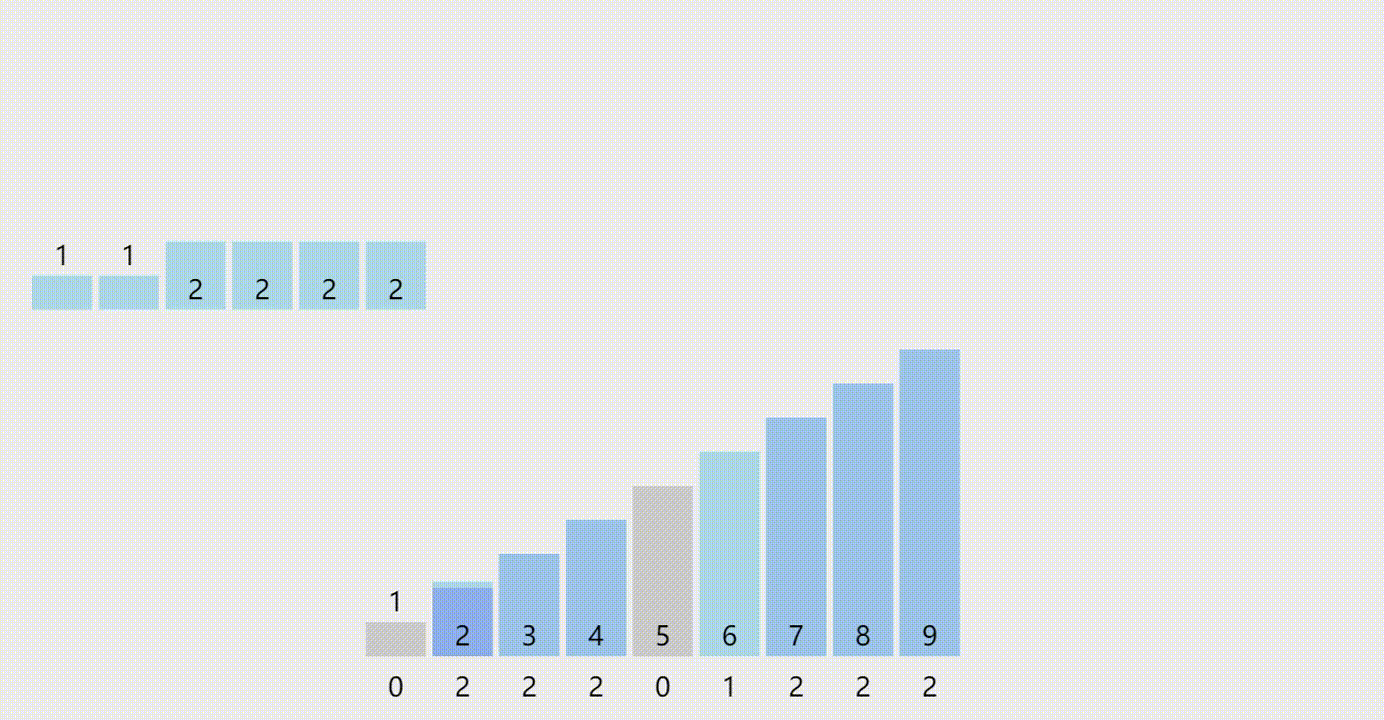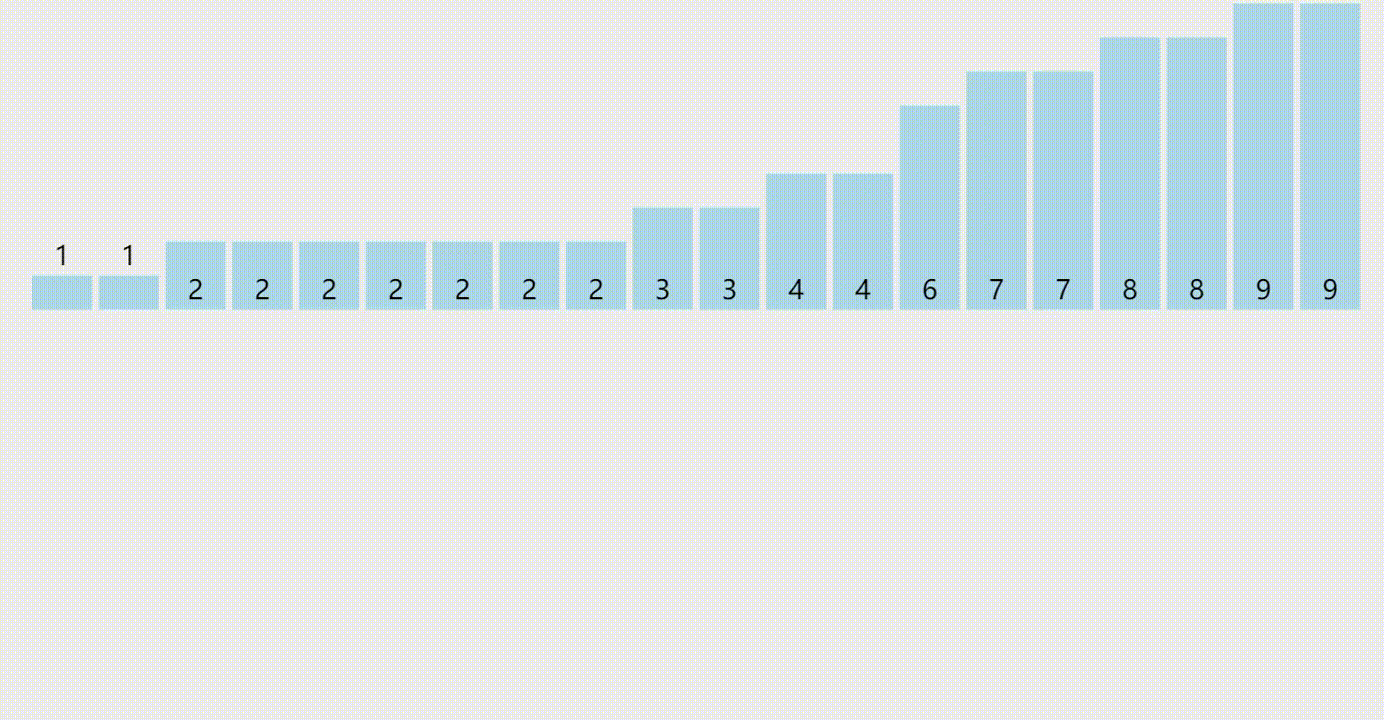
计数排序的原理
计数排序是一种非比较排序算法,它的核心思想是:对于每一个待排序的数,确定它在有序序列中的位置。
计数排序的基本步骤如下:
- 确定数列中数的范围,构造一个桶,桶的下标即为数的值。
- 扫描待排序的数列,对于每一个数,在桶中的对应位置+1。
- 对每一个桶,依次输出桶中所有数的个数,即可得到一个有序序列。
计数排序的时间复杂度为O(n),是一种非常高效的排序算法,但是它仅适用于数据范围不大的场景,因为它需要预先确定数列中数的范围,并且桶的大小也要相应的扩大。
下面是一个计数排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | #include <iostream>
#include <vector>
using namespace std;
void countSort(vector<int>& arr) {
int n = arr.size();
int max_element = *max_element(arr.begin(), arr.end());
vector<int> count(max_element + 1, 0);
for (int i = 0; i < n; i++) {
count[arr[i]]++;
}
int k = 0;
for (int i = 0; i <= max_element; i++) {
for (int j = 0; j < count[i]; j++) {
arr[k++] = i;
}
}
}
int main() {
vector<int> arr = {1, 4, 1, 2, 7, 5, 2};
cout << "Original array: \n";
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
countSort(arr);
cout << "\nSorted array: \n";
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了计数排序的基本功能:给定一个整数数组,将其从小到大排序,得到一个有序数组。
桶排序
桶排序的原理
桶排序是一种非比较型排序算法,它的基本思想是:将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。它是鸽巢排序的一种归纳结果。
桶排序的基本步骤如下:
- 设置一个定量的数组当作空桶子。
- 寻访序列,并且把每一个元素放入对应的桶子中。
- 对每个不是空的桶子进行排序。
- 从不是空的桶子里把项目再放回原来的序列中。
桶排序的时间复杂度为O(n+k),其中n是待排序数组的元素个数,k是桶的个数。在桶的数量较小时,桶排序是一个非常有效的排序算法。
下面是一个桶排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | #include <iostream>
#include <vector>
using namespace std;
void bucketSort(vector<double>& arr) {
int n = arr.size();
vector<vector<double>> buckets(n);
for (int i = 0; i < n; i++) {
int index = n * arr[i];
buckets[index].push_back(arr[i]);
}
for (int i = 0; i < n; i++) {
sort(buckets[i].begin(), buckets[i].end());
}
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < buckets[i].size(); j++) {
arr[index++] = buckets[i][j];
}
}
}
int main() {
vector<double> arr = {0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68};
cout << "Original array: \n";
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
bucketSort(arr);
cout << "\nSorted array: \n";
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
return 0;
}
|
这段代码实现了桶排序的基本功能:给定一个实数数组,将其从小到大排序,得到一个有序数组。
计数排序和桶排序的区别
计数排序和桶排序都是非比较类排序算法,它们的思想都是利用桶来进行排序。但是它们之间还是有一些区别的。
1.桶的数量不同:
计数排序需要一个计数数组,数组长度等于待排序数列的最大值加1,用来统计每个元素出现的次数。
而桶排序则需要一个桶数组,数组的长度要视具体情况而定,可以根据待排序数据的分布情况来确定,每个桶存放一定范围内的数据。
2.对元素的处理方式不同:
计数排序只是用来记录每个桶中存放的数据个数,而不是桶中存放的数据。每个桶中存放的都是相同的数据。因此,计数排序需要将每个元素统计出现的次数后,再进行元素排序。
桶排序则需要将每个元素按照一定规则分配到不同的桶中,并对每个桶中的数据进行排序。
3.时间和空间复杂度不同:
计数排序的时间复杂度为 O(n+k),其中 n 是待排序数列的长度,k 是数列中的最大值。计数排序需要额外的空间来存储计数数组,空间复杂度为 O(k)。
桶排序的时间复杂度为 O(n+k),其中 n 是待排序数列的长度,k 是桶的数量。桶排序需要额外的空间来存储桶数组,空间复杂度为 O(n+k)。
因此,当待排序数列的最大值和最小值差距较大时,适合使用桶排序。而当待排序数列的最大值和最小值差距不大,且数列长度较大时,适合使用计数排序。
基数排序

基数排序(Radix Sort)是一种非比较排序算法,它将数字按照每一位的大小来进行比较和排序,先从最低位开始排序,再到次低位,最后到最高位,排序完成后数字就变成了一个有序序列。基数排序是稳定排序算法,适用于待排序元素可以分割出独立的“位”来比较的数据类型,比如整数和字符串。以下是基数排序的C++代码实现:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | #include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 获取num的第d位数字,从低向高数第d位
int getDigit(int num, int d) {
int digit = 0;
for (int i = 1; i <= d; i++) {
digit = num % 10;
num /= 10;
}
return digit;
}
void radixSort(vector<int>& nums) {
if (nums.empty()) return;
int maxNum = *max_element(nums.begin(), nums.end()); // 找到数组中最大值
int maxDigit = 0;
while (maxNum > 0) { // 计算最大值的位数
maxNum /= 10;
maxDigit++;
}
vector<int> count(10); // 计数数组
vector<int> temp(nums.size()); // 临时数组
for (int d = 1; d <= maxDigit; d++) {
count.assign(10, 0); // 计数数组清零
for (int i = 0; i < nums.size(); i++) {
int digit = getDigit(nums[i], d); // 获取当前数字的第d位数字
count[digit]++; // 计数
}
for (int i = 1; i < count.size(); i++) {
count[i] += count[i-1]; // 求前缀和
}
for (int i = nums.size() - 1; i >= 0; i--) { // 从后往前遍历原数组,保证排序的稳定性
int digit = getDigit(nums[i], d); // 获取当前数字的第d位数字
temp[--count[digit]] = nums[i]; // 根据计数数组将原数组中的元素放入临时数组中
}
nums = temp; // 将排序后的临时数组赋值给原数组
}
}
int main() {
vector<int> nums = {53, 3, 542, 748, 14, 214, 154, 63, 616};
radixSort(nums);
for (auto x : nums) {
cout << x << " ";
}
cout << endl;
return 0;
}
|
希尔排序

希尔排序的原理
希尔排序是插入排序的一种改进版本。
希尔排序的思想是利用插入排序的特点,在插入排序的基础上,减少比较次数,从而提高排序效率。
希尔排序的基本思想是:将整个待排序的记录序列分割成为若干子序列分别进行插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次插入排序。
在希尔排序中,分割子序列的方法是:通过一个间隔(也称为增量)来划分记录,间隔从大到小递减。在第一趟排序中,每隔间隔个记录进行比较与交换;在第二趟排序中,间隔递减,再对每隔间隔个记录进行比较与交换;直到最后一趟排序时,间隔为1,此时整个序列基本有序,最后再进行一趟插入排序即可。
以下是希尔排序的 C++ 实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | #include<iostream>
using namespace std;
void shellSort(int arr[], int n)
{
// 增量 gap
for (int gap = n / 2; gap > 0; gap /= 2)
{
// 共 gap 个组
for (int i = gap; i < n; i++)
{
int j = i;
int temp = arr[i];
// 比较与交换,直到最前面
while (j >= gap && arr[j - gap] > temp)
{
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
}
int main()
{
int arr[] = {9, 6, 11, 3, 5, 12, 8, 7, 10, 15};
int n = sizeof(arr) / sizeof(arr[0]);
shellSort(arr, n);
cout << "排序后的数组:\n";
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
return 0;
}
|
本页面的全部内容在 小熊老师 - 莆田青少年编程俱乐部 0594codes.cn 协议之条款下提供,附加条款亦可能应用