10、搜索详解

搜索算法是一类用于在问题空间中查找解决方案的算法。以下是几种常见的搜索算法：

深度优先搜索（DFS）：从起点开始，尽可能远地探索每个可达节点，直到到达终点或无法继续前进为止。
广度优先搜索（BFS）：从起点开始，按照距离逐层探索所有可达节点，直到到达终点或搜索完整个图为止。
启发式搜索（Heuristic Search）：根据某种启发式函数估计节点到目标的距离，依次选取估价最小的节点进行扩展，直到找到解或搜索完整个图。
A*算法：结合了深度优先搜索和启发式搜索的特点，通过估价函数对搜索路径进行评估，以快速找到最佳路径。
迭代加深深度优先搜索（Iterative Deepening Depth-First Search, IDDFS）：在深度优先搜索的基础上，逐步增加最大搜索深度，直到找到目标节点。
双向搜索（Bidirectional Search）：从起点和终点同时开始搜索，直到两个搜索路径相遇为止。

这些搜索算法各有优缺点，选择合适的算法取决于具体问题的性质和规模。

搜索算法一般遵循以下几个步骤：

确定搜索空间：明确需要搜索的是什么，如一个图、一棵树，还是一个解空间等等。
选择搜索策略：根据问题的特性和目标，选择最合适的搜索策略。
执行搜索：根据所选择的策略，从起始节点开始，按照特定的顺序访问节点。
检查是否找到目标：每当访问一个新的节点时，都检查是否达到了目标。如果是，那么搜索结束。
处理搜索结果：根据搜索结果进行必要的处理，如打印路径、计算代价等。

以下是入门级两个搜索算法的详细介绍：

一、深度优先搜索

深度优先搜索（Depth-First Search，DFS）是一种常用的图遍历算法，也可以用于搜索树和图的路径等问题。DFS 从某个顶点开始遍历，沿着一条路径直到不能再前进，然后回溯到前一个节点，再继续遍历下一条路径。因此，DFS 可以用递归或栈来实现。

下面是 DFS 的基本思路和实现方法：

从起始节点开始，标记为已访问，并将其加入遍历路径。
遍历该节点的相邻节点，如果有未访问过的相邻节点，则将该相邻节点标记为已访问，将其加入遍历路径，并递归遍历该节点。
如果当前节点的所有相邻节点都已访问过，则回溯到上一个节点，继续遍历其未访问的相邻节点，直到遍历完所有节点。

下面是一个简单的使用递归实现的 DFS 的示例代码：

C++
#include <iostream>
#include <vector>

using namespace std;

void dfs(int u, vector<vector<int>>& adj, vector<bool>& visited, vector<int>& path) {
    visited[u] = true; // 标记该节点为已访问
    path.push_back(u); // 将该节点加入遍历路径
    for (int v : adj[u]) { // 遍历该节点的相邻节点
        if (!visited[v]) { // 如果相邻节点未被访问过
            dfs(v, adj, visited, path); // 递归遍历相邻节点
        }
    }
}

int main() {
    int n = 6; // 节点个数
    vector<vector<int>> adj(n); // 邻接表
    adj[0] = {1, 2};
    adj[1] = {0, 2, 3};
    adj[2] = {0, 1, 3};
    adj[3] = {1, 2, 4, 5};
    adj[4] = {3};
    adj[5] = {3};
    vector<bool> visited(n, false); // 标记节点是否已被访问
    vector<int> path; // 遍历路径
    dfs(0, adj, visited, path); // 从节点0开始遍历
    for (int u : path) {
        cout << u << " ";
    }
    cout << endl;
    return 0;
}

在上面的代码中，我们定义了一个邻接表 adj 来表示图，其中 adj[i] 表示节点 i 的所有相邻节点。我们使用一个 visited 数组来记录节点是否已被访问，使用一个 path 数组来记录遍历路径。然后从节点0开始遍历，调用 dfs 函数实现深度优先遍历。最后输出遍历路径。

需要注意的是，上面的实现方法是递归实现，如果图的深度过大，可能会导致栈溢出，因此需要使用迭代实现，或者使用系统栈（如 C++ 中的 stack`）来避免栈溢出。

下面是一个使用栈实现 DFS 的示例代码：

C++
#include <iostream>
#include <vector>
#include <stack>

using namespace std;

void dfs(int u, vector<vector<int>>& adj, vector<bool>& visited, vector<int>& path) {
    stack<int> s;
    s.push(u); // 将起始节点加入栈中
    while (!s.empty()) {
        int u = s.top();
        s.pop();
        if (!visited[u]) { // 如果节点未被访问过
            visited[u] = true; // 标记该节点为已访问
            path.push_back(u); // 将该节点加入遍历路径
            for (int v : adj[u]) { // 遍历该节点的相邻节点
                if (!visited[v]) { // 如果相邻节点未被访问过
                    s.push(v); // 将相邻节点加入栈中
                }
            }
        }
    }
}

int main() {
    int n = 6; // 节点个数
    vector<vector<int>> adj(n); // 邻接表
    adj[0] = {1, 2};
    adj[1] = {0, 2, 3};
    adj[2] = {0, 1, 3};
    adj[3] = {1, 2, 4, 5};
    adj[4] = {3};
    adj[5] = {3};
    vector<bool> visited(n, false); // 标记节点是否已被访问
    vector<int> path; // 遍历路径
    dfs(0, adj, visited, path); // 从节点0开始遍历
    for (int u : path) {
        cout << u << " ";
    }
    cout << endl;
    return 0;
}

在上面的代码中，我们使用一个栈 s 来存储待遍历的节点，初始时将起始节点加入栈中。然后在每次循环中，取出栈顶节点，并遍历其未访问过的相邻节点，将其加入栈中。需要注意的是，我们要在遍历相邻节点之前，先判断该节点是否已被访问过。

DFS 可以用于很多问题，如图的连通性判断、生成树、寻找路径等。需要根据具体的问题来选择合适的算法和实现方法。

示例：

考虑图G及其邻接列表，如下图所示。通过使用深度优先搜索(DFS)算法计算从节点H开始打印图的所有节点的顺序。

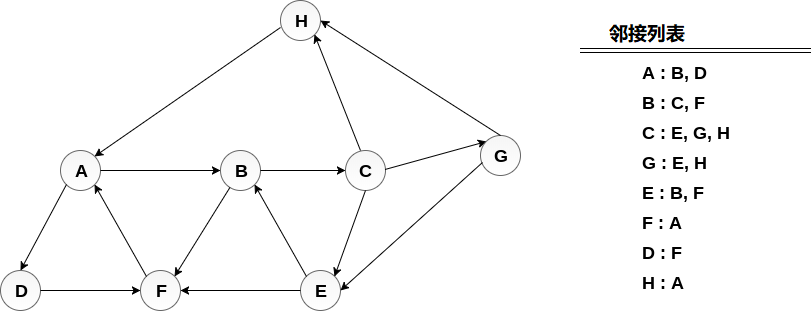
方案： 将H 推入堆栈 -

Text Only
STACK : H

弹出是堆栈的顶部元素，即H，打印它并将H的所有邻居推送到处于就绪状态的堆栈上。

Text Only
Print H   
STACK : A

弹出堆栈的顶部元素，即A，打印它并将A的所有邻居推入堆栈中处于就绪状态。

Text Only
Print A  
Stack : B, D

弹出堆栈的顶部元素，即D，打印它并将D的所有邻居推入处于就绪状态的堆栈。

Text Only
Print D   
Stack : B, F

弹出堆栈的顶部元素，即F，打印它并将F的所有邻居推入处于就绪状态的堆栈。

Text Only
Print F  
Stack : B

弹出堆栈的顶部，即B并推送所有邻居。

Text Only
Print B   
Stack : C

弹出堆栈的顶部，即C并推送所有邻居。

Text Only
Print C   
Stack : E, G

弹出堆栈的顶部，即G并推送其所有邻居。

Text Only
Print G  
Stack : E

弹出堆栈的顶部，即E并推送其所有邻居。

Text Only
Print E  
Stack :

因此，堆栈现在变为空，并且遍历了图的所有节点。

图表的打印顺序为：

Text Only
H → A → D → F → B → C → G → E

二、广度优先搜索

广度优先搜索（BFS，Breadth-First Search）是一种用于图遍历的算法，它从图的某个节点开始遍历，先访问该节点的所有相邻节点，再访问相邻节点的相邻节点，以此类推。换句话说，BFS 是按照节点的层次顺序来遍历图的。

BFS 的实现通常使用队列来辅助实现，每次从队列头部取出一个节点，访问该节点的所有相邻节点，并将这些相邻节点加入队列尾部。需要注意的是，BFS 可以用于无权图和有权图，但是对于有权图，需要使用优先队列来保证按照边权值从小到大访问相邻节点。

下面是一个使用队列实现 BFS 的示例代码：

C++
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

void bfs(int u, vector<vector<int>>& adj, vector<bool>& visited, vector<int>& path) {
    queue<int> q;
    q.push(u); // 将起始节点加入队列中
    visited[u] = true; // 标记该节点为已访问
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        path.push_back(u); // 将该节点加入遍历路径
        for (int v : adj[u]) { // 遍历该节点的相邻节点
            if (!visited[v]) { // 如果相邻节点未被访问过
                visited[v] = true; // 标记该节点为已访问
                q.push(v); // 将相邻节点加入队列中
            }
        }
    }
}

int main() {
    int n = 6; // 节点个数
    vector<vector<int>> adj(n); // 邻接表
    adj[0] = {1, 2};
    adj[1] = {0, 2, 3};
    adj[2] = {0, 1, 3};
    adj[3] = {1, 2, 4, 5};
    adj[4] = {3};
    adj[5] = {3};
    vector<bool> visited(n, false); // 标记节点是否已被访问
    vector<int> path; // 遍历路径
    bfs(0, adj, visited, path); // 从节点0开始遍历
    for (int u : path) {
        cout << u << " ";
    }
    cout << endl;
    return 0;
}

示例

考虑下图中显示的图G，计算从节点A到节点E的最小路径p。给定每条边的长度为1。

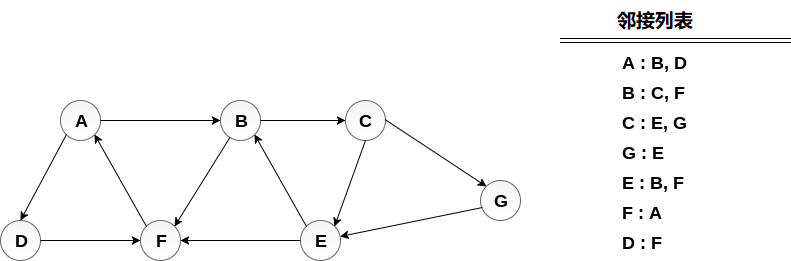
解答：

最小路径P可以通过应用广度优先搜索算法找到，该算法将从节点A开始并将以E结束。算法使用两个队列，即QUEUE1和QUEUE2。 QUEUE1保存要处理的所有节点，而QUEUE2保存从QUEUE1处理和删除的所有节点。

下面来看看节点A 中的图。

将A添加到QUEUE1，将NULL添加到QUEUE2。

Text Only
QUEUE1 = {A}  
QUEUE2 = {NULL}

从QUEUE1中删除节点A并插入其所有邻居，将节点A插入QUEUE2。

Text Only
QUEUE1 = {B, D}  
QUEUE2 = {A}

从QUEUE1中删除节点B并插入其所有邻居。将节点B插入QUEUE2。

Text Only
QUEUE1 = {D, C, F}   
QUEUE2 = {A, B}

从QUEUE1中删除节点D并插入其所有邻居。由于F是已插入的唯一邻居，因此不会再插入它。将节点D插入QUEUE2。

Text Only
QUEUE1 = {C, F}  
QUEUE2 = { A, B, D}

从QUEUE1中删除节点C并插入其所有邻居。将节点C添加到QUEUE2。

Text Only
QUEUE1 = {F, E, G}  
QUEUE2 = {A, B, D, C}

从QUEUE1中删除F并添加其所有邻居。由于已经添加了所有邻居，不会再添加它们。将节点F添加到QUEUE2。

Text Only
QUEUE1 = {E, G}  
QUEUE2 = {A, B, D, C, F}

从QUEUE1中删除E，所有E的邻居都已添加到QUEUE1，因此不会再添加它们。访问所有节点，并且目标节点即E遇到QUEUE2。

Text Only
QUEUE1 = {G}  
QUEUE2 = {A, B, D, C, F,  E}

现在，使用QUEUE2中可用的节点从E回溯到A。

最小路径为：A→B→C→E。

三、搜索算法的常见案例

图的遍历：在这种情况下，深度优先搜索和广度优先搜索都很常用。例如，你可能需要找出从一个节点到另一个节点的路径，或者找出图中的所有连通分量。
最短路径问题：这是图论中的经典问题，需要找出从一个节点到另一个节点的最短路径。Dijkstra算法和A*算法在这种情况下非常有用。
解决滑动拼图问题：在这个问题中，你需要找出一系列的移动，这些移动能将拼图从一个状态移动到另一个状态。这个问题可以用A*算法解决，其中启发式函数是当前状态和目标状态之间的曼哈顿距离。
寻找迷宫的出路：在这种情况下，你可以使用深度优先搜索或广度优先搜索来查找从入口到出口的路径。广度优先搜索在找到解后，保证了找到的是最短路径。
八皇后问题：这是一个经典的回溯搜索问题，需要在8x8的棋盘上放置8个皇后，使得没有任何两个皇后在同一行、同一列或同一对角线上。
数独问题：这是另一个常见的回溯搜索问题。需要填充9x9的网格，使得每行、每列和每个3x3的子网格中都包含数字1到9。

本页面的全部内容在 小熊老师 - 莆田青少年编程俱乐部 0594codes.cn 协议之条款下提供，附加条款亦可能应用