3、数据结构
3.1 线性表
线性表是一种常见的数据结构,它是由n个数据元素a1,a2,……,an(n>=0)组成的有限序列,其中数据元素的个数称为线性表的长度。线性表的两种基本存储结构是顺序存储结构和链式存储结构。
在 C++ 中,可以使用数组和链表等数据结构来实现线性表。
数组是一种在内存中连续存储数据的数据结构,可以通过数组下标来访问其中的元素,也就是顺序存储结构。
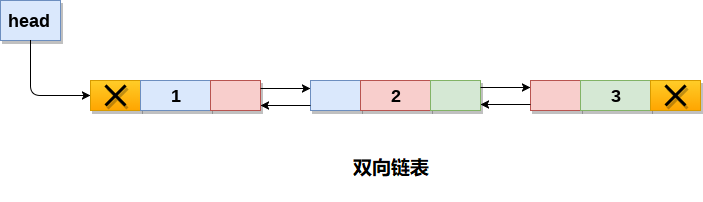
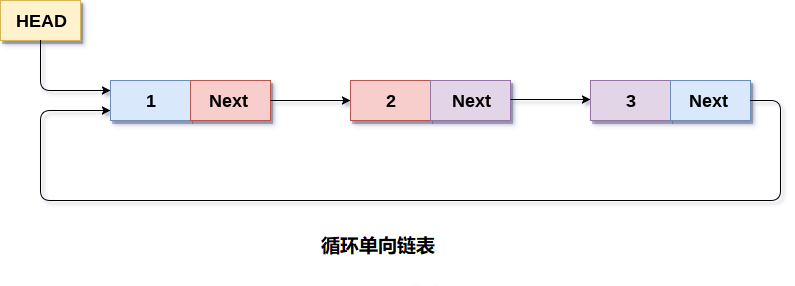
链表是一种通过指针来连接的数据结构,可以分为单向链表、双向链表、循环链表等。链表中每个节点都包含了数据和指向下一个节点的指针,它的内存空间可以是不连续的,也就是链式存储结构。
在 C++ STL 中,也提供了许多现成的线性表容器,如 vector、list、deque 等,它们分别以顺序存储和链式存储的方式实现了线性表的基本操作。这些容器有着高效的实现和方便的接口,可以大大简化程序设计和开发过程。
3.1.1 链表:单链表、双向链表、循环链表
链表是一种常见的数据结构,用于存储一系列具有相同类型的数据元素。C++ 中的链表有三种类型:单向链表、双向链表和循环链表。
单向链表(Singly Linked List)是最简单的链表形式,它的每个节点都只有一个指向下一个节点的指针。在 C++ 中,单向链表可以使用结构体和类实现。
下面是一个单向链表的结构体实现示例:
C++ struct Node {
int data ;
Node * next ;
Node ( int d ) : data ( d ), next ( NULL ) {}
};
这里定义了一个 Node 结构体,包含一个 int 类型的 data 成员变量和一个指向下一个节点的指针 next。构造函数 Node(int d) 可以用于初始化节点的数据。
双向链表(Doubly Linked List)是每个节点都有两个指针,一个指向前一个节点,一个指向下一个节点。在 C++ 中,双向链表同样可以使用结构体和类实现。
下面是一个双向链表的结构体实现示例:
C++ struct Node {
int data ;
Node * prev ;
Node * next ;
Node ( int d ) : data ( d ), prev ( NULL ), next ( NULL ) {}
};
这里定义了一个 Node 结构体,包含一个 int 类型的 data 成员变量和指向前一个节点和下一个节点的指针 prev 和 next。构造函数 Node(int d) 可以用于初始化节点的数据。
循环链表(Circular Linked List)是一种特殊的链表形式,它的最后一个节点指向头结点,形成一个环。循环链表同样可以使用结构体和类实现。
下面是一个循环链表的结构体实现示例:
C++ struct Node {
int data ;
Node * next ;
Node ( int d ) : data ( d ), next ( NULL ) {}
};
这里同样定义了一个 Node 结构体,和单向链表的结构体实现示例相同,不同之处在于最后一个节点的 next 指向头结点。
链表的操作包括遍历、插入、删除、查找等,需要根据具体情况选择不同的方法和算法。
以下是单链表的常见操作:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87 #include <iostream>
using namespace std ;
//定义单链表节点结构体
struct ListNode {
int val ;
ListNode * next ;
ListNode ( int x ) : val ( x ), next ( NULL ) {}
};
//链表遍历
void traverseList ( ListNode * head ) {
ListNode * curr = head ;
while ( curr ) {
cout << curr -> val << " " ;
curr = curr -> next ;
}
cout << endl ;
}
//链表插入(在头部插入)
ListNode * insertAtHead ( ListNode * head , int val ) {
ListNode * newNode = new ListNode ( val );
newNode -> next = head ;
return newNode ;
}
//链表插入(在尾部插入)
ListNode * insertAtTail ( ListNode * head , int val ) {
ListNode * newNode = new ListNode ( val );
if ( ! head ) {
return newNode ;
}
ListNode * curr = head ;
while ( curr -> next ) {
curr = curr -> next ;
}
curr -> next = newNode ;
return head ;
}
//链表删除(删除指定值的节点)
ListNode * deleteNode ( ListNode * head , int val ) {
ListNode * dummy = new ListNode ( -1 );
dummy -> next = head ;
ListNode * curr = dummy ;
while ( curr -> next ) {
if ( curr -> next -> val == val ) {
ListNode * temp = curr -> next ;
curr -> next = curr -> next -> next ;
delete temp ;
} else {
curr = curr -> next ;
}
}
return dummy -> next ;
}
//链表查找(查找指定值的节点)
ListNode * searchList ( ListNode * head , int val ) {
ListNode * curr = head ;
while ( curr ) {
if ( curr -> val == val ) {
return curr ;
}
curr = curr -> next ;
}
return NULL ;
}
int main () {
ListNode * head = NULL ;
head = insertAtHead ( head , 1 );
head = insertAtHead ( head , 2 );
head = insertAtHead ( head , 3 );
head = insertAtTail ( head , 4 );
traverseList ( head ); // 3 2 1 4
head = deleteNode ( head , 2 );
traverseList ( head ); // 3 1 4
ListNode * node = searchList ( head , 1 );
if ( node ) {
cout << "Found node: " << node -> val << endl ;
} else {
cout << "Node not found" << endl ;
}
return 0 ;
}
这里我们定义了单链表的节点结构体ListNode,包含节点的值val和下一个节点的指针next。我们使用traverseList函数来遍历链表,将链表的节点值输出。insertAtHead函数用于在链表的头部插入一个节点,insertAtTail函数用于在链表的尾部插入一个节点,deleteNode函数用于删除指定值的节点,searchList函数用于查找指定值的节点。在main函数中,我们测试了链表的插入、删除、查找和遍历等操作。
以下是双向链表的一些基本操作,包括创建链表、遍历链表、在链表中插入节点、在链表中删除节点等。
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105 #include <iostream>
using namespace std ;
struct ListNode {
int val ;
ListNode * prev ;
ListNode * next ;
ListNode ( int x ) : val ( x ), prev ( nullptr ), next ( nullptr ) {}
};
// 创建双向链表
ListNode * createList ( int n ) {
if ( n <= 0 ) return nullptr ;
ListNode * head = nullptr , * tail = nullptr ;
for ( int i = 1 ; i <= n ; i ++ ) {
int x ;
cin >> x ;
if ( ! head ) {
head = tail = new ListNode ( x );
} else {
tail -> next = new ListNode ( x );
tail -> next -> prev = tail ;
tail = tail -> next ;
}
}
return head ;
}
// 遍历双向链表
void printList ( ListNode * head ) {
ListNode * cur = head ;
while ( cur ) {
cout << cur -> val << " " ;
cur = cur -> next ;
}
cout << endl ;
}
// 在链表中插入一个节点
ListNode * insertNode ( ListNode * head , int pos , int val ) {
ListNode * newNode = new ListNode ( val );
if ( pos == 0 ) {
newNode -> next = head ;
if ( head ) head -> prev = newNode ;
return newNode ;
}
ListNode * cur = head ;
for ( int i = 1 ; i < pos ; i ++ ) {
cur = cur -> next ;
if ( ! cur ) return head ;
}
newNode -> prev = cur ;
newNode -> next = cur -> next ;
if ( cur -> next ) cur -> next -> prev = newNode ;
cur -> next = newNode ;
return head ;
}
// 在链表中删除一个节点
ListNode * deleteNode ( ListNode * head , int pos ) {
if ( ! head ) return nullptr ;
if ( pos == 0 ) {
ListNode * newHead = head -> next ;
if ( newHead ) newHead -> prev = nullptr ;
delete head ;
return newHead ;
}
ListNode * cur = head ;
for ( int i = 1 ; i < pos ; i ++ ) {
cur = cur -> next ;
if ( ! cur ) return head ;
}
ListNode * delNode = cur -> next ;
if ( ! delNode ) return head ;
cur -> next = delNode -> next ;
if ( delNode -> next ) delNode -> next -> prev = cur ;
delete delNode ;
return head ;
}
int main () {
ListNode * head = createList ( 5 );
printList ( head );
head = insertNode ( head , 3 , 6 );
printList ( head );
head = deleteNode ( head , 1 );
printList ( head );
return 0 ;
}
上述代码中定义了一个 ListNode 结构体,它包含一个 val 变量,以及一个前驱指针 prev 和一个后继指针 next,这三个变量分别指向链表中的前一个节点和后一个节点。然后定义了一些函数,包括创建链表、遍历链表、在链表中插入节点、在链表中删除节点等。
下面是循环链表的一些基本操作及对应的 C++ 代码:
1.创建一个循环链表
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 struct ListNode {
int val ;
ListNode * next ;
ListNode ( int x ) : val ( x ), next ( NULL ) {}
};
ListNode * createCircularList ( int * a , int n ) {
if ( n == 0 ) return NULL ;
ListNode * head = new ListNode ( a [ 0 ]);
ListNode * pre = head ;
for ( int i = 1 ; i < n ; i ++ ) {
ListNode * cur = new ListNode ( a [ i ]);
pre -> next = cur ;
pre = cur ;
}
pre -> next = head ; // 最后一个节点指向头节点,形成环形结构
return head ;
}
2.遍历循环链表
C++ void traverseCircularList ( ListNode * head ) {
if ( ! head ) return ;
ListNode * cur = head ;
do {
cout << cur -> val << " " ;
cur = cur -> next ;
} while ( cur != head );
}
3.在循环链表中查找某个值
C++ 1
2
3
4
5
6
7
8
9
10
11
12 ListNode * searchCircularList ( ListNode * head , int val ) {
if ( ! head ) return NULL ;
ListNode * cur = head ;
do {
if ( cur -> val == val ) {
return cur ;
}
cur = cur -> next ;
} while ( cur != head );
return NULL ;
}
4.在循环链表中插入节点
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 void insertCircularList ( ListNode * & head , int val ) {
ListNode * cur = new ListNode ( val );
if ( ! head ) { // 空链表,新节点即为头节点
head = cur ;
head -> next = head ;
return ;
}
ListNode * tail = head ;
while ( tail -> next != head ) {
tail = tail -> next ;
}
tail -> next = cur ;
cur -> next = head ;
if ( val < head -> val ) { // 插入头节点的情况
head = cur ;
}
}
5.在循环链表中删除节点
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 void deleteCircularList ( ListNode * & head , int val ) {
if ( ! head ) return ;
ListNode * pre = NULL ;
ListNode * cur = head ;
while ( cur -> val != val ) {
if ( cur -> next == head ) { // 未找到值为 val 的节点
return ;
}
pre = cur ;
cur = cur -> next ;
}
if ( cur == head ) { // 删除头节点的情况
head = head -> next ;
pre = head ;
while ( pre -> next != cur ) {
pre = pre -> next ;
}
pre -> next = head ;
} else {
pre -> next = cur -> next ;
}
delete cur ;
}
3.1.2 栈
栈(stack)是一种线性数据结构,具有后进先出(LIFO)的特点,即最后压入的元素最先弹出。
栈的两个主要操作是压入和弹出。压入操作通常称为入栈(push),弹出操作通常称为出栈(pop)。
栈的特点使得它在一些算法和计算机程序中非常有用。例如,它可以用来解决括号匹配问题、计算表达式、实现深度优先搜索等。
在C++中,栈可以使用STL容器stack来实现,也可以手动实现。
STL容器stack的实现:
STL中的stack是一个容器适配器,它以特定的方式包装了底层容器,使其表现为一个堆栈(后进先出)数据结构。STL提供了一个名为的头文件,其中定义了一个类模板stack,可以用来创建不同类型的堆栈对象。
stack提供了以下主要函数:
push(): 将元素推入堆栈的顶部。
pop(): 弹出堆栈顶部的元素。
top(): 返回堆栈顶部的元素。
empty(): 如果堆栈为空,则返回true;否则返回false。
size(): 返回堆栈中元素的数量。
stack使用底层容器来实现堆栈,缺省情况下使用deque容器,也可以使用vector和list容器。在创建堆栈对象时,可以指定使用的容器类型。
下面是一个使用STL stack的简单示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 #include <iostream>
#include <stack>
using namespace std ;
int main ()
{
stack < int > s ;
s . push ( 10 );
s . push ( 20 );
s . push ( 30 );
cout << "The top element of stack is: " << s . top () << endl ;
s . pop ();
cout << "The top element of stack is: " << s . top () << endl ;
cout << "The size of stack is: " << s . size () << endl ;
return 0 ;
}
输出:
C++ The top element of stack is : 30
The top element of stack is : 20
The size of stack is : 2
在上面的示例中,我们首先创建了一个int类型的堆栈对象s,然后使用push()函数将三个元素10、20和30推入堆栈中。然后使用top()函数输出堆栈顶部的元素,弹出堆栈顶部的元素,再次输出堆栈顶部的元素,最后输出堆栈中元素的数量。
需要注意的是,由于STL stack是基于底层容器实现的,因此在使用时要根据实际情况选择合适的容器类型。如果对于栈的大小变化不确定,需要频繁地在栈顶插入或删除元素,建议使用deque容器实现的stack。如果栈的大小已知,且只在栈顶插入或删除元素,建议使用vector容器实现的stack,因为vector在随机访问方面更高效。如果需要在任意位置插入或删除元素,建议使用list容器实现的stack。
Stack使用数组手动实现:
以下是用数组实现栈的 C++ 代码示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66 #include <iostream>
using namespace std ;
const int MAX_SIZE = 100 ; // 定义栈的最大长度
class Stack {
private :
int top ; // 栈顶指针
int data [ MAX_SIZE ]; // 存储数据的数组
public :
Stack (); // 构造函数
bool isEmpty (); // 判断栈是否为空
bool isFull (); // 判断栈是否已满
void push ( int x ); // 压入数据
int pop (); // 弹出栈顶元素
int getTop (); // 获取栈顶元素
};
Stack :: Stack () {
top = -1 ; // 初始化栈顶指针为-1
}
bool Stack :: isEmpty () {
return top == -1 ;
}
bool Stack :: isFull () {
return top == MAX_SIZE - 1 ;
}
void Stack :: push ( int x ) {
if ( isFull ()) {
cout << "栈已满,无法添加数据!" << endl ;
return ;
}
data [ ++ top ] = x ; // 将数据x压入栈顶
}
int Stack :: pop () {
if ( isEmpty ()) {
cout << "栈为空,无法弹出数据!" << endl ;
return -1 ;
}
return data [ top -- ]; // 弹出栈顶元素
}
int Stack :: getTop () {
if ( isEmpty ()) {
cout << "栈为空,无法获取栈顶元素!" << endl ;
return -1 ;
}
return data [ top ]; // 获取栈顶元素
}
int main () {
Stack s ; // 定义一个栈对象
s . push ( 1 );
s . push ( 2 );
s . push ( 3 );
cout << s . pop () << endl ; // 输出3
cout << s . pop () << endl ; // 输出2
cout << s . getTop () << endl ; // 输出1
s . push ( 4 );
cout << s . getTop () << endl ; // 输出4
return 0 ;
}
上述代码实现了一个栈的基本功能:压入数据、弹出数据、获取栈顶元素等操作。其中,栈的最大长度定义为常量 MAX_SIZE,栈内部用一个数组来存储数据。由于栈是后进先出(LIFO)的数据结构,所以每次压入数据时,我们要将数据压入栈顶;每次弹出数据时,我们要从栈顶弹出数据。
Stack 使用链表手动实现:
以下是栈用链表实现的 C++ 代码示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74 #include <iostream>
using namespace std ;
template < typename T >
class Node
{
public :
T data ;
Node < T > * next ;
Node ( T data ) : data ( data ), next ( nullptr ) {}
};
template < typename T >
class Stack
{
public :
Stack () : head ( nullptr ) {}
~ Stack () { clear (); }
void push ( T data )
{
Node < T > * new_node = new Node < T > ( data );
new_node -> next = head ;
head = new_node ;
}
void pop ()
{
if ( empty ())
return ;
Node < T > * temp = head ;
head = head -> next ;
delete temp ;
}
T top () const
{
if ( empty ())
throw "Stack is empty" ;
return head -> data ;
}
bool empty () const { return head == nullptr ; }
void clear ()
{
while ( head )
{
Node < T > * temp = head ;
head = head -> next ;
delete temp ;
}
}
private :
Node < T > * head ;
};
int main ()
{
Stack < int > s ;
s . push ( 1 );
s . push ( 2 );
s . push ( 3 );
while ( ! s . empty ())
{
cout << s . top () << " " ;
s . pop ();
}
cout << endl ;
return 0 ;
}
该代码使用了链表来实现栈的基本操作,包括 push,pop,top 和 empty 等。在栈顶插入元素时,我们使用一个新的节点来存储该元素,并将其 next 指针指向当前的栈顶元素,然后将新节点设为新的栈顶元素。在弹出栈顶元素时,我们需要将栈顶元素的 next 指针指向下一个元素,然后删除当前的栈顶元素。在获取栈顶元素时,我们需要检查栈是否为空,如果为空则抛出异常。最后,我们需要清空栈中的所有元素,以避免内存泄漏。
3.1.3 队列
队列(queue)是一种先进先出(First In First Out,FIFO)的线性数据结构,类似于现实生活中排队的情况。它有两个基本操作:入队(Enqueue)和出队(Dequeue)。在队列中,新的元素只能在队列的一端(尾部)添加,而现有的元素只能从队列的另一端(头部)删除。队列的应用非常广泛,如操作系统中的进程调度、网络数据传输等。
在 C++ STL 中,队列是容器适配器,它的底层实现可以是一个单向链表、双向链表或者数组。
常见的队列操作包括:
push(element):将元素 element 添加到队列的尾部。
pop():移除队列头部的元素。
front():返回队列头部的元素,但不移除它。
back():返回队列尾部的元素,但不移除它。
empty():判断队列是否为空。
size():返回队列中元素的数量。
下面是一个使用 STL queue 实现队列的简单示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 #include <iostream>
#include <queue>
using namespace std ;
int main () {
queue < int > q ;
// 添加元素到队列尾部
q . push ( 1 );
q . push ( 2 );
q . push ( 3 );
// 返回队列头部元素并移除
cout << q . front () << endl ; // 输出 1
// 移除队列头部元素
q . pop ();
// 返回队列头部元素
cout << q . front () << endl ; // 输出 2
// 返回队列尾部元素
cout << q . back () << endl ; // 输出 3
// 判断队列是否为空
cout << ( q . empty () ? "队列为空" : "队列不为空" ) << endl ;
// 返回队列中元素的数量
cout << "队列中元素的数量:" << q . size () << endl ;
return 0 ;
}
输出结果为:
以上代码中,queue<int> 创建了一个整型队列对象。使用 push() 函数向队列中添加元素,使用 pop() 函数移除队列头部元素,使用 front() 函数返回队列头部元素但不移除它,使用 back() 函数返回队列尾部元素但不移除它,使用 empty() 函数判断队列是否为空,使用 size() 函数返回队列中元素的数量。
队列使用数组手动实现:
以下是使用数组实现队列操作的 C++ 代码示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87 #include <iostream>
#define MAXSIZE 100 // 定义队列最大长度
using namespace std ;
class Queue {
private :
int queue [ MAXSIZE ];
int front , rear ;
public :
Queue () {
front = -1 ;
rear = -1 ;
}
bool isFull () {
return ( rear == MAXSIZE - 1 );
}
bool isEmpty () {
return ( front == -1 || front > rear );
}
void enqueue ( int data ) {
if ( isFull ()) {
cout << "Queue is full \n " ;
return ;
}
rear ++ ;
queue [ rear ] = data ;
if ( front == -1 ) {
front = 0 ;
}
}
void dequeue () {
if ( isEmpty ()) {
cout << "Queue is empty \n " ;
return ;
}
front ++ ;
}
int getFront () {
if ( isEmpty ()) {
cout << "Queue is empty \n " ;
return -1 ;
}
return queue [ front ];
}
int getRear () {
if ( isEmpty ()) {
cout << "Queue is empty \n " ;
return -1 ;
}
return queue [ rear ];
}
void printQueue () {
if ( isEmpty ()) {
cout << "Queue is empty \n " ;
return ;
}
cout << "Queue is: " ;
for ( int i = front ; i <= rear ; i ++ ) {
cout << queue [ i ] << " " ;
}
cout << endl ;
}
};
int main () {
Queue q ;
q . enqueue ( 10 );
q . enqueue ( 20 );
q . enqueue ( 30 );
q . enqueue ( 40 );
q . printQueue ();
q . dequeue ();
q . dequeue ();
q . printQueue ();
cout << "Front element is: " << q . getFront () << endl ;
cout << "Rear element is: " << q . getRear () << endl ;
return 0 ;
}
此代码定义了一个 Queue 类,使用数组实现了队列的基本操作,包括入队、出队、判断队列是否为空、判断队列是否已满等。在 main 函数中,展示了如何使用该队列,包括入队、出队、获取队首元素和队尾元素等操作。
队列使用链表手动实现:
下面是使用链表实现队列的 C++ 代码:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70 #include <iostream>
using namespace std ;
// 定义链表节点
struct Node {
int data ;
Node * next ;
Node ( int data ) : data ( data ), next ( nullptr ) {}
};
// 队列类
class Queue {
private :
Node * front ;
Node * rear ;
public :
Queue () : front ( nullptr ), rear ( nullptr ) {}
// 入队
void enqueue ( int data ) {
Node * node = new Node ( data );
if ( rear == nullptr ) {
front = rear = node ;
return ;
}
rear -> next = node ;
rear = node ;
}
// 出队
void dequeue () {
if ( front == nullptr ) {
return ;
}
Node * temp = front ;
front = front -> next ;
if ( front == nullptr ) {
rear = nullptr ;
}
delete temp ;
}
// 获取队头元素
int peek () {
if ( front == nullptr ) {
return -1 ;
}
return front -> data ;
}
// 队列是否为空
bool empty () {
return front == nullptr ;
}
};
int main () {
Queue q ;
q . enqueue ( 1 );
q . enqueue ( 2 );
q . enqueue ( 3 );
q . enqueue ( 4 );
q . enqueue ( 5 );
while ( ! q . empty ()) {
cout << q . peek () << " " ;
q . dequeue ();
}
cout << endl ;
return 0 ;
}
这里采用了尾插法,即新加入的节点作为队列的队尾。出队操作从队头开始,如果队列为空,则直接返回。获取队头元素和判断队列是否为空都是在队头节点上进行的。
3.2 简单树
3.2.1 树的定义及其相关概念
树是一种重要的数据结构,它是由n(n≥1)个节点组成的有限集合。树具有以下特点:
每个节点都只有一个父节点,根节点除外。
每个节点可以有多个子节点,但它们之间没有先后关系,也就是说这些子节点之间是平等的。
根节点是树的唯一入口。
每个节点可以存储一个或多个数据元素,称为该节点的数据域。
树的常见术语有:
节点的度:一个节点拥有的子树的个数称为该节点的度。
叶子节点:度为0的节点称为叶子节点,也叫终端节点。
非终端节点:度不为0的节点称为非终端节点,也叫分支节点或内部节点。
树的度:树中节点的度的最大值称为树的度。
节点的层次:根节点为第一层,根节点的子节点为第二层,以此类推。
树的深度:树中节点的最大层次称为树的深度或高度。
祖先节点和子孙节点:如果从一个节点到另一个节点有路径相连,那么这个路径上的所有节点都是这个节点的祖先节点,而这个节点称为后代节点。
兄弟节点:具有相同父节点的节点称为兄弟节点。
子树:节点和它的后代节点构成的集合称为子树。
树可以有很多种不同的形式,其中常见的包括二叉树、平衡树、B树、B+树等。每种树都有其特定的应用场景和优缺点。
3.2.2 树的父亲表示法
树的父亲表示法(Parent Representation)是一种表示树的数据结构,也称为父指针表示法。该方法是将每个节点除了根节点外,都指向它的父节点,根节点没有父节点。
在父亲表示法中,每个节点包括两个信息:数据和一个指向其父节点的指针。对于根节点,指针为空或者指向一个特殊节点。
使用父亲表示法表示一棵树时,可以很方便地找到一个节点的父节点,但查找子节点却不太方便。同时,该方法不适合表示多叉树。
以下是用C++实现树的父亲表示法的示例代码:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 #include <iostream>
#include <vector>
using namespace std ;
const int MAXN = 1005 ; // 树的最大结点数
vector < int > son [ MAXN ]; // 存储每个结点的儿子结点
int main ()
{
int n ;
cin >> n ;
// 读入每个结点的父亲结点
for ( int i = 1 ; i <= n ; i ++ ) {
int father ;
cin >> father ;
if ( father == -1 ) {
continue ;
}
son [ father ]. push_back ( i );
}
// 遍历每个结点的儿子结点
for ( int i = 1 ; i <= n ; i ++ ) {
cout << "Node " << i << "'s sons: " ;
for ( int j = 0 ; j < son [ i ]. size (); j ++ ) {
cout << son [ i ][ j ] << " " ;
}
cout << endl ;
}
return 0 ;
}
上述代码中,son 数组表示每个结点的儿子结点,数组下标为结点的编号,每个元素是一个 vector<int>,存储该结点的所有儿子结点。在读入每个结点的父亲结点后,将该结点添加到父亲结点的儿子结点中,即将结点编号添加到 son[father] 的末尾。最后遍历每个结点的儿子结点,输出它们的编号。
3.3.3 二叉树的定义及其基本性质
二叉树是一种树形结构,其中每个节点最多有两个子节点,分别为左子节点和右子节点。每个节点的子节点是有顺序的,左子节点在前,右子节点在后。
二叉树的基本性质有:
一个二叉树的深度为k,当且仅当它的各个层次有节点数分别为\(1,2,4,……,2^{k-1}\) 。
对于一颗非空二叉树,如果叶子节点数为n0,度数为2的节点数为n2,则\(n0=n2+1\) 。
对于一颗非空二叉树,如果深度为k,且有\(2^k-1\) 个节点,则其上各节点都满足:若编号为i(1≤i≤\(2^k-1\) ),则其左子节点编号为2i,右子节点编号为2i+1;其父节点编号为i/2。
对于一颗非空二叉树,如果叶子节点数为n0,度数为1的节点数为n1,则\(n0=n1+1\) 。
若对一颗有n个节点的完全二叉树(深度为k),按照层次标号(从上到下,从左到右),对于任意的i(1≤i≤n),有:
(1)i=1时,为根,无父节点,i>1时,其父节点编号为i/2。
(2)如果2i>n,则i无左子节点;否则其左子节点的编号为2i。
(3)如果2i+1>n,则i无右子节点;否则其右子节点的编号为2i+1。
在二叉树中,根节点是没有父节点的节点,叶子节点是没有子节点的节点。深度为k的二叉树的最大节点数为\(2^{k}-1\) 。
3.2.4 二叉树的孩子表示法
二叉树的孩子表示法是指,在二叉树中,每个节点不仅有左右子树,而且还保存了指向其孩子节点的指针,这种表示方法被称为孩子表示法。
在孩子表示法中,每个节点包含了指向其孩子节点的指针,通常包括指向左儿子节点的指针和指向右儿子节点的指针,如果节点没有左儿子或右儿子,则相应的指针为 NULL。
使用孩子表示法可以方便地进行遍历和查找等操作。例如,前序遍历二叉树时,可以按照先访问根节点、再访问左子树、最后访问右子树的顺序进行遍历,这可以通过访问节点的左右孩子节点实现。
下面是一个使用孩子表示法的二叉树节点结构体定义:
C++ struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( NULL ), right ( NULL ) {}
};
在这个结构体中,val 表示节点的值,left 和 right 分别表示指向左右孩子节点的指针。构造函数用于初始化节点的值和孩子节点指针。
3.2.5 二叉树的遍历:前序、中序、后序遍历
二叉树的遍历是指按照一定的顺序遍历二叉树中的所有节点。常见的遍历方式有前序遍历、中序遍历和后序遍历。
前序遍历(pre-order traversal):先访问根节点,然后按照先左后右的顺序递归遍历左右子树。
中序遍历(in-order traversal):先递归遍历左子树,然后访问根节点,最后递归遍历右子树。
后序遍历(post-order traversal):先递归遍历左右子树,然后访问根节点。
下面是二叉树遍历的C++实现:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58 #include <iostream>
using namespace std ;
// 二叉树的节点
struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( NULL ), right ( NULL ) {}
};
// 前序遍历
void preorderTraversal ( TreeNode * root ) {
if ( ! root ) return ;
cout << root -> val << " " ;
preorderTraversal ( root -> left );
preorderTraversal ( root -> right );
}
// 中序遍历
void inorderTraversal ( TreeNode * root ) {
if ( ! root ) return ;
inorderTraversal ( root -> left );
cout << root -> val << " " ;
inorderTraversal ( root -> right );
}
// 后序遍历
void postorderTraversal ( TreeNode * root ) {
if ( ! root ) return ;
postorderTraversal ( root -> left );
postorderTraversal ( root -> right );
cout << root -> val << " " ;
}
int main () {
TreeNode * root = new TreeNode ( 1 );
root -> left = new TreeNode ( 2 );
root -> right = new TreeNode ( 3 );
root -> left -> left = new TreeNode ( 4 );
root -> left -> right = new TreeNode ( 5 );
root -> right -> left = new TreeNode ( 6 );
root -> right -> right = new TreeNode ( 7 );
cout << "前序遍历: " ;
preorderTraversal ( root );
cout << endl ;
cout << "中序遍历: " ;
inorderTraversal ( root );
cout << endl ;
cout << "后序遍历: " ;
postorderTraversal ( root );
cout << endl ;
return 0 ;
}
输出结果:
C++ 前序遍历 : 1 2 4 5 3 6 7
中序遍历 : 4 2 5 1 6 3 7
后序遍历 : 4 5 2 6 7 3 1
3.3 特殊树
3.3.1 完全二叉树的定义与基本性质
完全二叉树是指除了最后一层节点外,每一层的节点数都达到最大值,并且最后一层节点都尽量靠左排列的二叉树。
完全二叉树的基本性质如下:
对于深度为k的完全二叉树,其节点总数为\(2^k-1\) 。
除了最后一层外,每一层上的节点数均达到最大值,最后一层上的节点都集中在该层最左边的若干位置。
若设二叉树的深度为h,则其前\(h-1\) 层为一棵满二叉树,第\(h\) 层从左到右有若干个节点,且所有节点都连续集中在最左边的若干位置。
若设二叉树的深度为\(h\) ,节点总数为\(n\) ,则第\(h\) 层上至少有\(n-2^{h-1}+1\) 个节点,最多有\(2^h-1\) 个节点。
一棵完全二叉树可以用数组来表示,对于第\(i\) 个节点,其左子节点为\(2i\) ,右子节点为\(2i+1\) ,其父节点为\(i/2\) (当\(i\) 为偶数时为\(i/2\) ,当\(i\) 为奇数时为\((i-1)/2\) )。
3.3.2 完全二叉树的数组表示法
完全二叉树可以使用数组表示,假设完全二叉树的深度为 \(d\) ,则:
数组的下标从 1 开始,即根节点的下标为 1。
第 \(i\) 个节点的左儿子下标为 \(2i\) ,右儿子下标为 \(2i+1\) 。
对于 \(i\leq\lfloor\frac{n}{2}\rfloor\) 的节点,其下标为 \(i\) 的节点的父节点下标为 \(\lfloor\frac{i}{2}\rfloor\) 。
其中,\(n\) 表示完全二叉树中节点的总个数。
使用数组表示完全二叉树可以方便地进行遍历等操作,但是需要注意的是,如果存在节点数小于数组长度的情况,空闲的数组元素应该被填充为默认值(比如 -1)或者直接忽略。
以下是一个完全二叉树的数组表示法的实现代码示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 #include <iostream>
#include <vector>
using namespace std ;
// 返回该节点的父亲节点
int parent ( int i ) {
return ( i - 1 ) / 2 ;
}
// 返回该节点的左儿子节点
int leftChild ( int i ) {
return 2 * i + 1 ;
}
// 返回该节点的右儿子节点
int rightChild ( int i ) {
return 2 * i + 2 ;
}
int main () {
// 完全二叉树的数组表示法
vector < int > tree { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 };
// 输出第 i 个节点的父亲、左右儿子节点
int i = 3 ;
cout << "节点 " << tree [ i ] << " 的父亲节点是 " << tree [ parent ( i )] << endl ;
cout << "节点 " << tree [ i ] << " 的左儿子节点是 " << tree [ leftChild ( i )] << endl ;
cout << "节点 " << tree [ i ] << " 的右儿子节点是 " << tree [ rightChild ( i )] << endl ;
return 0 ;
}
在这个代码中,我们使用了一个 vector 来表示一个完全二叉树,根据完全二叉树的数组表示法,对于节点 i,其父亲节点为 (i - 1) / 2,左儿子节点为 2 * i + 1,右儿子节点为 2 * i + 2。最后,我们输出了第 3 个节点的父亲、左右儿子节点。输出结果为:
C++ 节点 4 的父亲节点是 1
节点 4 的左儿子节点是 9
节点 4 的右儿子节点是 10
这表明,节点 4 的父亲节点是 1,左儿子节点是 9,右儿子节点是 10,与完全二叉树的数组表示法的定义相符。
3.3.3 哈夫曼树的定义、构造及其遍历
哈夫曼树是一种特殊的二叉树,它的构造是基于字符频率的,其中出现频率高的字符拥有更短的编码,而出现频率低的字符拥有更长的编码,从而最大限度地减少了编码长度,节省了存储空间。
哈夫曼树的构造过程如下:
将字符按照出现频率从小到大排序,构造一个只包含每个字符节点的森林。
取出频率最小的两个字符节点,将它们合并为一个新的节点,权值为两个节点权值之和,并将该新节点插入到森林中。
重复步骤2,直到森林中只剩下一个树,即哈夫曼树构造完成。
哈夫曼树的遍历包括前序、中序和后序遍历,具体实现如下:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 // 哈夫曼树结点的定义
struct HuffmanNode {
char data ; // 结点存储的字符
int freq ; // 字符出现的频率
HuffmanNode * left ; // 左孩子指针
HuffmanNode * right ; // 右孩子指针
HuffmanNode ( char c = '\0' , int f = 0 , HuffmanNode * l = nullptr , HuffmanNode * r = nullptr ) : data ( c ), freq ( f ), left ( l ), right ( r ) {}
};
// 前序遍历
void preOrder ( HuffmanNode * root ) {
if ( ! root ) {
return ;
}
cout << root -> data << "(" << root -> freq << ") " ;
preOrder ( root -> left );
preOrder ( root -> right );
}
// 中序遍历
void inOrder ( HuffmanNode * root ) {
if ( ! root ) {
return ;
}
inOrder ( root -> left );
cout << root -> data << "(" << root -> freq << ") " ;
inOrder ( root -> right );
}
// 后序遍历
void postOrder ( HuffmanNode * root ) {
if ( ! root ) {
return ;
}
postOrder ( root -> left );
postOrder ( root -> right );
cout << root -> data << "(" << root -> freq << ") " ;
}
其中,HuffmanNode结构体定义了哈夫曼树的结点,包含字符、频率和左右孩子指针。preOrder、inOrder和postOrder函数分别实现了前序、中序和后序遍历,对于每个结点,输出它的字符和频率。
3.3.4 二叉树的定义及构造
二叉树是一种树形结构,其中每个节点最多只有两个子节点。具体来说,一个二叉树可以为空,或者由一个根节点和两个分别称为左子树和右子树的二叉树组成。
在C++中,可以使用以下结构体来定义二叉树的节点:
C++ struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( NULL ), right ( NULL ) {}
};
其中,val代表节点的值,left和right分别指向左子树和右子树。
二叉树的构造可以使用递归的方式进行,例如:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14 TreeNode * buildTree ( vector < int >& inorder , vector < int >& postorder ) {
if ( inorder . empty () || postorder . empty ()) return NULL ;
int root_val = postorder . back ();
auto root_pos = find ( inorder . begin (), inorder . end (), root_val );
int left_size = root_pos - inorder . begin ();
TreeNode * root = new TreeNode ( root_val );
vector < int > left_inorder ( inorder . begin (), root_pos );
vector < int > right_inorder ( root_pos + 1 , inorder . end ());
vector < int > left_postorder ( postorder . begin (), postorder . begin () + left_size );
vector < int > right_postorder ( postorder . begin () + left_size , postorder . end () - 1 );
root -> left = buildTree ( left_inorder , left_postorder );
root -> right = buildTree ( right_inorder , right_postorder );
return root ;
}
该代码实现了通过中序遍历和后序遍历构造二叉树的功能。在具体实现中,首先找到后序遍历的最后一个元素作为根节点,然后在中序遍历中找到根节点的位置,进而将中序遍历和后序遍历分别划分为左右两个子树的遍历序列。接着递归构造左右子树,并将它们分别作为根节点的左右子树。最后返回根节点即可。
下面是另一份使用递归方式构造二叉树的 C++ 代码示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 #include <iostream>
using namespace std ;
// 二叉树节点定义
struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( NULL ), right ( NULL ) {}
};
// 递归构造二叉树
TreeNode * buildTree ( int prestart , int instart , int inend , vector < int >& preorder , vector < int >& inorder ) {
// 如果子树为空,返回 NULL
if ( prestart > preorder . size () - 1 || instart > inend ) {
return NULL ;
}
// 根据前序遍历的顺序,当前子树的根节点为前序遍历序列的第一个元素
TreeNode * root = new TreeNode ( preorder [ prestart ]);
// 在中序遍历序列中寻找当前根节点的位置
int inIndex = 0 ;
for ( int i = instart ; i <= inend ; i ++ ) {
if ( inorder [ i ] == root -> val ) {
inIndex = i ;
}
}
// 根据中序遍历序列的顺序,左子树在 inIndex 左边,右子树在 inIndex 右边
root -> left = buildTree ( prestart + 1 , instart , inIndex - 1 , preorder , inorder );
root -> right = buildTree ( prestart + inIndex - instart + 1 , inIndex + 1 , inend , preorder , inorder );
return root ;
}
// 前序遍历二叉树
void preorderTraversal ( TreeNode * root ) {
if ( root == NULL ) {
return ;
}
cout << root -> val << " " ;
preorderTraversal ( root -> left );
preorderTraversal ( root -> right );
}
int main () {
vector < int > preorder = { 3 , 9 , 20 , 15 , 7 };
vector < int > inorder = { 9 , 3 , 15 , 20 , 7 };
TreeNode * root = buildTree ( 0 , 0 , inorder . size () - 1 , preorder , inorder );
cout << "前序遍历结果:" ;
preorderTraversal ( root );
return 0 ;
}
在上述代码中,我们定义了二叉树节点结构体 TreeNode,其中包括节点的值 val,左右子节点指针 left 和 right。在 buildTree 函数中,我们使用前序遍历序列和中序遍历序列来构造二叉树,其中 prestart、instart 和 inend 分别表示当前子树在前序遍历序列和中序遍历序列中的起始和结束位置。
3.4 简单图
3.4.1 图的定义及其相关概念
图是由若干个顶点和连接这些顶点的边组成的一种数据结构,通常用G=(V,E)表示,其中V为顶点集合,E为边集合。顶点之间的连线称为边,一条边连接的两个顶点称为邻接点,一个顶点的度数是其邻接点的数量。
在图的基础上,还有以下几个相关概念:
有向图和无向图:如果图的每一条边都是单向的,那么这个图就是有向图,否则就是无向图。
权重图和非权重图:如果图的边有权值,那么这个图就是权重图,否则就是非权重图。
连通图和非连通图:如果图中任意两个顶点都有一条路径相连,那么这个图就是连通图,否则就是非连通图。对于无向图而言,若任意两个顶点间都有路径相连,则称该无向图为连通无向图。
强连通图和弱连通图:如果有向图中任意两个顶点都有双向路径相连,那么这个图就是强连通图,否则就是弱连通图。
子图和生成子图:如果一个图的部分顶点和边可以组成一个新的图,那么这个新的图就是原图的子图。如果一个图的一部分顶点和边可以组成一个联通图,那么这个新的图就是原图的生成子图。
度数和入度出度:一个顶点的度数是指与这个顶点相邻的边的数量。对于有向图而言,每个顶点有入度和出度两个概念,入度是指以该顶点为终点的边的数量,出度是指以该顶点为起点的边的数量。
3.4.2 图的邻接矩阵存储
图的邻接矩阵存储是一种常用的图的存储方式,主要适用于稠密图,即边数相对于顶点数较多的情况。它的基本思想是将图中的顶点用一个一维数组存储,将边用一个二维数组(邻接矩阵)来表示,邻接矩阵中的元素表示两个顶点之间是否有边相连。
具体来说,邻接矩阵存储需要用一个二维数组G[V][V],其中V表示顶点数。如果顶点i和顶点j之间有边相连,则G[i][j]等于1,否则为0(或者其他设定的表示方式)。如果该图是有权图,则可以将G[i][j]表示为i到j的边的权重值。
邻接矩阵存储的优点是对于判断任意两个顶点之间是否有边相连非常方便,只需要查询数组中对应元素的值即可。同时,由于采用数组存储,可以快速定位某个顶点的信息,具有很好的随机访问性能。缺点是对于稀疏图,即边数相对于顶点数较少的情况,会造成存储空间的浪费。
下面是一个简单的C++代码示例,用邻接矩阵存储表示一个无向图:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 const int MAXN = 100 ;
int G [ MAXN ][ MAXN ]; //邻接矩阵存储
int main () {
int n , m ; //n表示顶点数,m表示边数
cin >> n >> m ;
memset ( G , 0 , sizeof ( G )); //初始化为0
//读入m条边
for ( int i = 0 ; i < m ; i ++ ) {
int u , v ;
cin >> u >> v ;
G [ u ][ v ] = G [ v ][ u ] = 1 ; //无向图,两个方向都要标记
}
//输出邻接矩阵
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 1 ; j <= n ; j ++ ) {
cout << G [ i ][ j ] << " " ;
}
cout << endl ;
}
return 0 ;
}
这段代码中,首先读入顶点数n和边数m,然后通过二重循环读入每条边的起点和终点,并将对应的G[u][v]和G[v][u]标记为1,表示这两个顶点之间有边相连。最后,通过两重循环输出邻接矩阵。
3.4.3 图的邻接表存储
图的邻接表存储方式是一种常见的图的存储方式。该存储方式将图中每个顶点的所有邻接点存储在一个链表中,因此需要为每个顶点创建一个链表。如果是有向图,那么每个顶点可以有一个出边链表和一个入边链表。
具体实现时,可以用一个数组来表示整个图,数组中的每个元素都是一个链表的头指针。链表中的每个结点表示一个边,包括该边的终点和权值等信息。下面是一个示例:
C++ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 #include <iostream>
#include <vector>
#include <list>
using namespace std ;
// 定义图的邻接表存储结构
class Graph {
public :
Graph ( int n ) : adjList ( n ) {}
// 添加一条边
void addEdge ( int u , int v ) {
adjList [ u ]. push_back ( v );
adjList [ v ]. push_back ( u );
}
// 打印邻接表
void print () const {
for ( int i = 0 ; i < adjList . size (); ++ i ) {
cout << "Vertex " << i << ": " ;
for ( auto j : adjList [ i ]) {
cout << j << " " ;
}
cout << endl ;
}
}
private :
vector < list < int >> adjList ; // 存储邻接表
};
int main () {
Graph g ( 5 );
g . addEdge ( 0 , 1 );
g . addEdge ( 0 , 2 );
g . addEdge ( 1 , 3 );
g . addEdge ( 1 , 4 );
g . addEdge ( 2 , 3 );
g . print ();
return 0 ;
}
输出结果为:
C++ Vertex 0 : 1 2
Vertex 1 : 0 3 4
Vertex 2 : 0 3
Vertex 3 : 1 2
Vertex 4 : 1
其中,每一行的格式为 Vertex i: v1 v2 ...,表示顶点 i 的相邻顶点为 v1、v2 等。由于是无向图,因此每条边都要在两个顶点的链表中都存储一遍。
小熊老师 - 莆田青少年编程俱乐部 0594codes.cn 协议之条款下提供,附加条款亦可能应用